少し冒険して、円管層流のヌセルト数を求めてみよう!:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(16)(3/5 ページ)
微分方程式を解こう
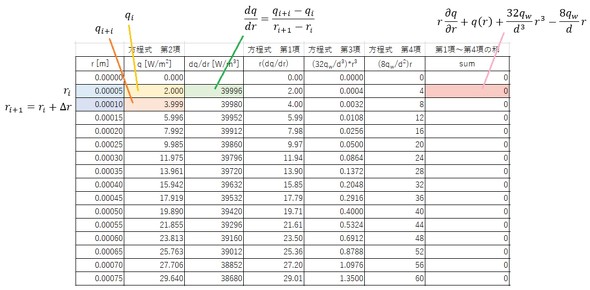
微分方程式の式16は導出できたものの、筆者の数学力ではこの解は分かりません。そこで、筆者お気に入りのExcel積分で探りを入れてみましょう。図4は、そのExcel積分シートです。
半径方向座標を刻み幅Δrで分割し、Δrピッチで縦方向に並べます。r=0[m]の熱流束はゼロなので、その値を代入しておきます。i=iでの熱流束qiが求まったとき、次のqi+1を求めることが目標です。
図示した式を使ってdq/drを計算し、微分方程式式16の各項を評価します。これらの総和を求めるセルを作成し、その合計がゼロになるように(つまり、方程式が成り立つように)、Excelのゴールシーク機能を使ってqi+1を求めます。この作業を、全てのrの位置で実行していきます。
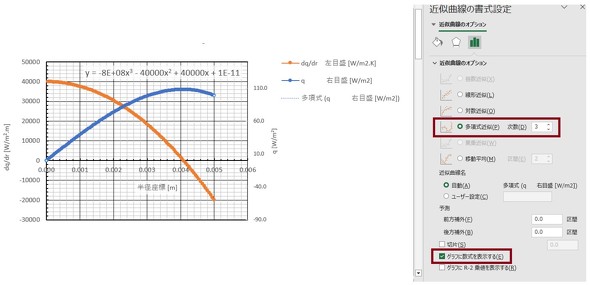
取りあえず、数値的に求まった熱流束と、その半径方向での微分をグラフにしてみました。図5に示します。
続いて、Excelの近似曲線機能を使って近似式を求めます。熱流束qのグラフについては、多項式近似の次数が3のときにぴたりと一致しました。つまり、方程式の解はrの3次式で表されるようです。
方程式の解として式17を仮定しましょう。rの3次式です。
半径座標微分は式18となります。
式17と式18を、式16に代入して整理すると、次のようになります。
これがどのようなrであっても成立するということは、r2の係数がゼロ、r0の係数がゼロでなければなりません。これらをゼロとした次式からAとBが求まります。
少し自信がありませんが、方程式の解は次のようになるはずです。
では、確認してみましょう。r=0のとき、q=0になるはずです。代入してみます。
確かにそうなりました。次に、r=d/2のとき、q=qwになるはずです。こちらも代入してみましょう。
おおっ、こちらも合っています。式16をあらためて見ると、第1項はrの割り算なので、q(r)のrの次数を1つ下げています。第2項は微分なので、やはり次数が1つ下がります。そして第3項はrの2次式、第4項は定数。つまり、式16の右辺は、rの3次式と1次式の和になっていることに、この時点でぱっと気付くべきでした。
温度分布を求める
フーリエの法則によれば、熱流束を積分したものが温度分布になります。
上式に式21を代入して、計算を進めていきましょう。
次に、以下の境界条件を代入して積分定数を求めます。
積分定数が求まりました。これを式27に代入しておきます。
後の計算を簡単にするために、定数Fを設定しました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

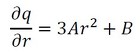 式18
式18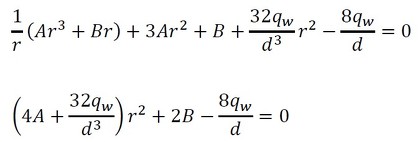 式19
式19 式20
式20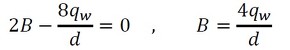 式21
式21 式22
式22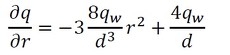 式23
式23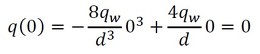 式24
式24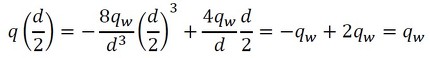 式25
式25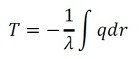 式26
式26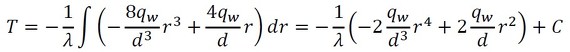 式27
式27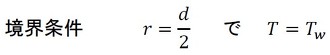 式28
式28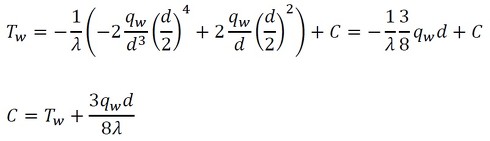 式29
式29 式30
式30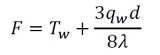 式31
式31





