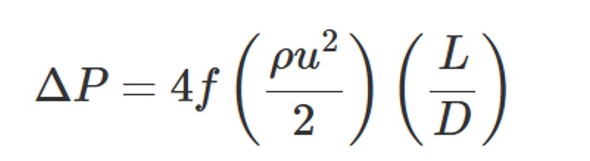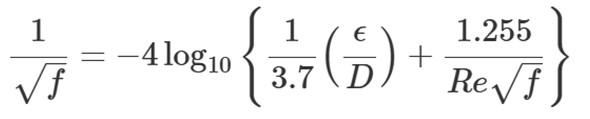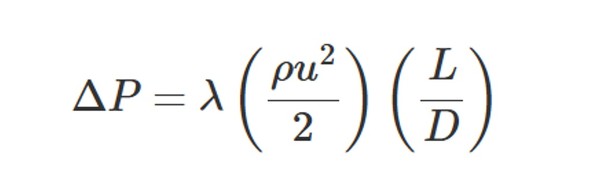配管流れの基本的な計算方法：はじめての化学工学（5）（2/2 ページ）

[かねまる，MONOist]

レイノルズ数による層流と乱流の予測

　配管内の流れを考える時、レイノルズ数（Re）を用いて流れの状態を判断します。レイノルズ数は流れが層流か乱流かを予測する無次元量です。慣性力と粘性力の比はDuρ/μとして定義されます。

図4 レイノルズ数。D：配管内径［m］、u：流速［m/s］、ρ：密度［kg/m3］、μ：粘度［Pa・s］［クリックで拡大］

　一般に、Reが2100以下の場合は層流、4000以上の場合は乱流と見なされ、2100〜4000の範囲は遷移流として不安定な状態であるとされます。つまり層流においては粘性力が、乱流においては慣性力が流れを支配していることを意味します。

• Re <= 2100（層流）：流れ方向に対して平行で、乱れが少ない
• 2100 < Re < 4000（遷移領域）：層流と乱流の間で不安定に変動し、予測困難な挙動を示す
• Re >= 4000（乱流）：流れ方向に対して直行する流れや渦が生じる

圧力損失の考慮

　配管内を流れる流体には、大きく分けて2種類のエネルギー損失が生じます。損失エネルギーを圧力換算して圧力損失とも呼ばれます。1つ目は配管内壁との摩擦、2つ目は配管継手が引き起こす流れの乱れです。

　1つ目の配管内壁との摩擦による圧力損失は、ファニングの式やダルシーワイズバッハの式を用いて計算できます。

図5 ファニングの式。ΔP：圧力損失［Pa］、f：管摩擦係数［-］、ρ：密度［kg/m3］、u：流速［m/s］、L：配管長さ［m］、D：配管内径［m］［クリックで拡大］

　式中に記載の管摩擦係数fは配管内壁の粗さやレイノルズ数によって変化する値です。層流においてはf=16/Reの式が成り立ちます。対して乱流域ははさまざまな式で表せます。特に用いられるのがコールブルックの式です。

図6 コールブルックの式。f：管摩擦係数［-］、ε：配管粗さ［m］D：配管内径［m］、Re：レイノルズ数［-］［クリックで拡大］

　その他にもブラウジウスの式、ニクラゼの式、プラントル・カルマンの式などがあります。計算から求める以外にも、レイノルズ数と相対粗度から管摩擦係数が簡単に分かるムーディー線図という図があります。化学工学会が発行している化学工学便覧の他、さまざまな参考書に記載されています。

　ファニングの式における管摩擦係数を4fからλに表記を変えることでダルシーワイズバッハの式に変化します。つまり式の意味は同じです。

図7 ダルシーワイズバッハの式。ΔP：圧力損失［Pa］、λ：管摩擦係数［-］、ρ：密度［kg/m3］、u：流速［m/s］、L：配管長さ［m］、D：配管内径［m］［クリックで拡大］

　2つ目の配管継手が引き起こす流れの乱れは、配管継手（エルボ、ティー、バルブ、レジューサなど）の内部での渦発生などが原因です。この場合、係数nを用いてL＝nDを計算することで、その損失量を直管の相当長に換算します。同じ継手が複数個ある場合は、その個数分だけ相当長を加算します。相当長でファニングの式やダルシーワイズバッハの式で計算します。

　例えば90度エルボは32、玉型弁（全開）は300です。こちらの値もムーディー線図と同様に、化学工学便覧の他、さまざまな参考書に記載されています。

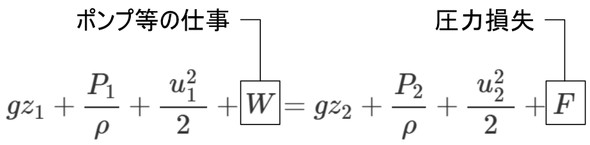
　ベルヌーイの定理は外部からの仕事や圧力損失は考慮されていません。このため、圧力損失F、そしてポンプやブロワなどから加える仕事Wを補正項として加えることで実用的な計算が可能になります。

図8 ベルヌーイの定理の補正［クリックで拡大］

---

まとめ

　今回は、化学プラントにおける配管設計の基礎として、配管内を流れる流体の挙動を計算する方法を紹介しました。連続の式とベルヌーイの定理を理解し、レイノルズ数によって流れの状態を把握することが重要です。

　また、配管設計においては、摩擦や配管継手による圧力損失を考慮する必要があります。これらの知識を踏まえて、適切な配管径やポンプの選定を行うことが、プロセス設計の第一歩になります。

⇒ 連載バックナンバーはこちら

筆者代表紹介

かねまる

プラント技術の解説サイト「ケムファク」を運営。大学院まで化学を専攻し、現在は化学メーカーの生産技術職に従事。