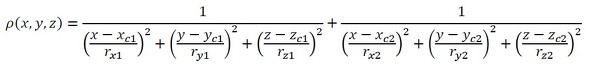フリーソフトでボルトの疲労破断の有無を予測する:CAEを正しく使い疲労強度計算と有機的につなげる(18)(5/6 ページ)
STLファイルの作成
トポロジー最適化ソフトを作るのだったら、最適化結果をSTL形式で出力し、他の3D CADで読み込めるようにしたいですね。その手順を述べます。
3D CADによる立体の定義方法ですが、多くは「B-reps(boundary representation)」と呼ばれる方法で行われています。物体の中と物体の外の境界は必ず面があるはずなので、この面(境界面)の集合で物体を表現できます。このような物体の定義方法をB-repsと言います。初めてこの言葉を知ったのは、米国のSDRC(Structural Dynamics Research Corporation)が「GEOMOD」というソリッドモデラーを発表したときでした。SDRCは“CAE(Computer Aided Engineering)”という用語を初めて使った会社だったと記憶しています。今でいう3D CADですが、コンピュータ上で立体の切った貼ったができることはちょっとしたカルチャーショックでした。図21にB-repsのイメージを示します。
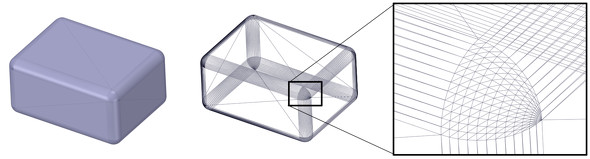
STL形式はB-reps方式で立体を表現します。図22にSTL形式のイメージを示します。STL形式では曲面を使わずに三角形の面だけを使います。面の数が非常に多くなりました。円弧面などは多角形近似となります。
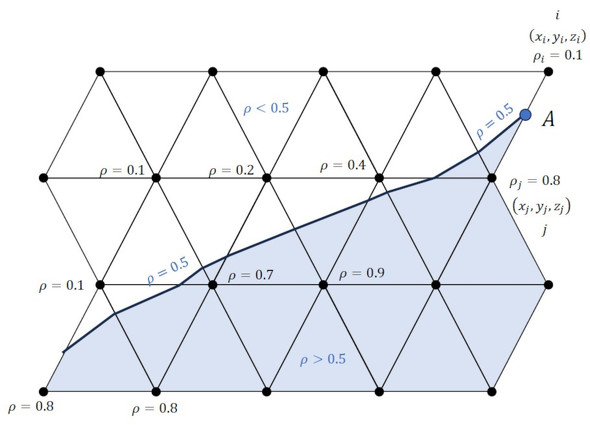
トポロジー最適化の結果をSTL形式に変換する場合、それぞれの要素が持つ密度という属性を使って境界面を作ります。図23にトポロジー最適化に使用した要素と節点、各節点の密度値および境界面を示します。密度は要素の属性だったのですが、連載第5回で説明した要素解と節点解の関係と同じ考え方で、各節点にも密度値を割り当てました。
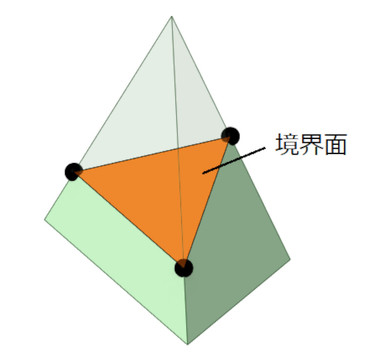
境界面の密度値を0.5[-]としましょう。図23のA点に注目します。A点は節点iと節点jをつなぐ線上にあります。節点iの密度値は0.1[-]、節点jの密度値は0.8[-]、境界面の密度値は0.5[-]とすると、密度値の比から線形補間でA点の座標値が決まります。A点のような中間点をつなぐことで境界面を作ることができます。図24に、このようにして作った境界面を示します。もともと四面体要素なので境界面は必ず三角形になってくれます。
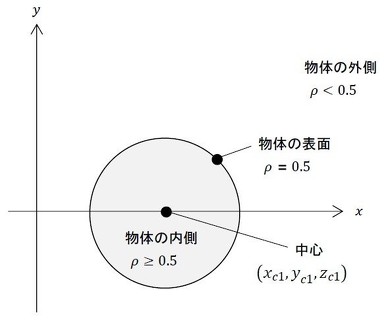
図23において、物体内部はρ≧0.5[-]、物体外部はρ<0.5[-]だということは、図23の状態では物体の形状は密度値で決まっています。つまり、密度がある値以上の点は物体の内側となります。この考え方はコンピュータグラフィックスの黎明(れいめい)期に使われていた「メタボール」による物体の定義方法となります。映画『ターミネーター2』に登場する液体金属製の敵ロボットはメタボールですね。図25にメタボールによる物体定義方法を示します。例えば、式8のような形で座標の関数として密度を定義します。
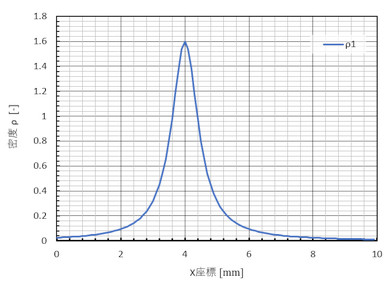
図26にx軸上の密度の変化を示します。
ではあと1つ密度を定義して足し算しましょう(式9)。
図27にx軸上の密度の変化を示します。
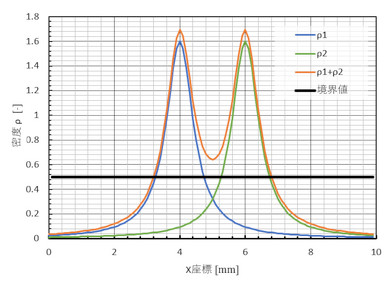
では、式9で定義された物体はというと、図28のようになります。プニュっと引っ付きました。
物体の陰影の表現のためには表面の外向き法線ベクトルを求める必要があります。式10で求められます(参考文献[1])。
太字はベクトルを表し、iはx軸と同じ方向を向く大きさ1のベクトル(基底ベクトル)、逆三角はハミルトン演算子でした。
参考文献:
- [1]矢野健太郎|解析学概論|裳華房(S53)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞

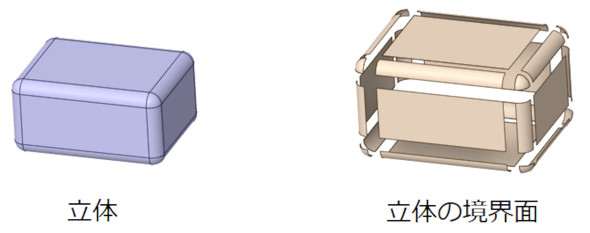
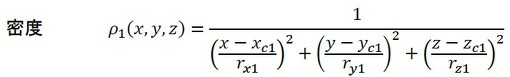 式8
式8