フリーソフトでボルトの疲労破断の有無を予測する：CAEを正しく使い疲労強度計算と有機的につなげる（18）（3/6 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

フリーソフト「LISA」でやってみよう

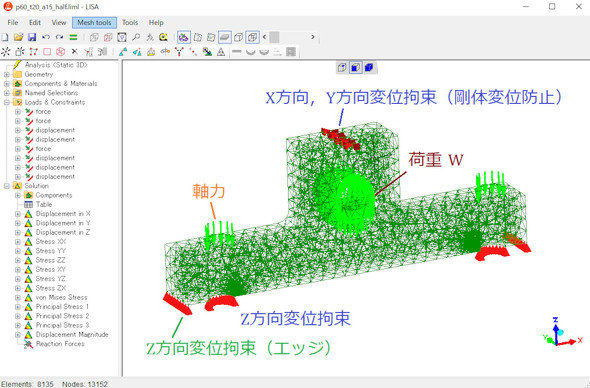
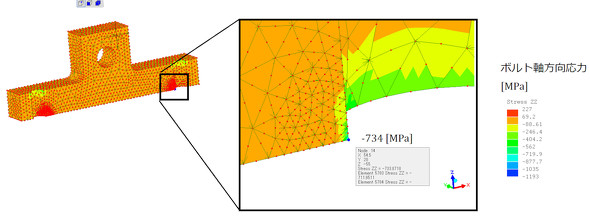
　図5の境界条件は、LISAでも簡単に設定できます。図9にLISAによる解析画面を、図10にボルト軸方向応力分布を示します。図9では図示しやすいように2分の1対称モデルとしましたが、1分の1モデルでも同じ結果となります。

図9　LISAによる解析画面［クリックで拡大］

図10　ボルト軸方向応力分布：LISA［クリックで拡大］

　図10のA点の応力はマイナス値なので、開口なしと判断できます。

応力がマイナスならボルトは疲労破断しないと判断できるか

　開口判定位置の応力がマイナス（圧縮応力）ならボルトは疲労破断しないと判断できるでしょうか。サーベイをしてみましょう。以下の手順で調べてみました。

1. ボルト穴エッジの応力がちょうどゼロとなる荷重を求める
2. 接触要素を用い、ボルト軸力を再現させたモデルでボルトに発生する応力振幅を求める
3. 式2を用いて安全率を求める

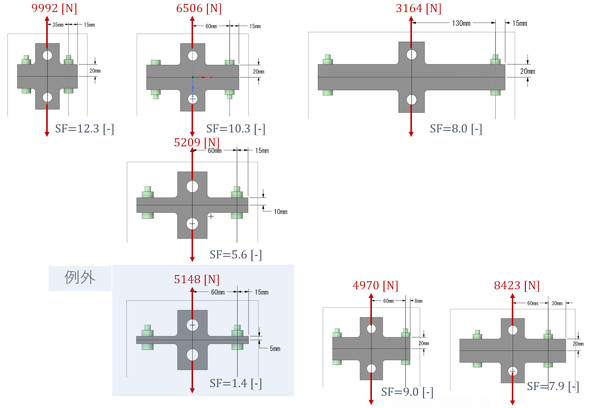
　図11にボルト穴エッジの応力がちょうどゼロとなる荷重（これはLISAで求めました）とその荷重での安全率（これは連載第17回の方法で求めました）を示します。

図11　ボルト穴エッジの応力がちょうどゼロとなる荷重での安全率［クリックで拡大］

　例外が1つありますが、ボルト穴エッジの応力がちょうどゼロとなる荷重では安全率は2［-］以上あるとの結果となりました。

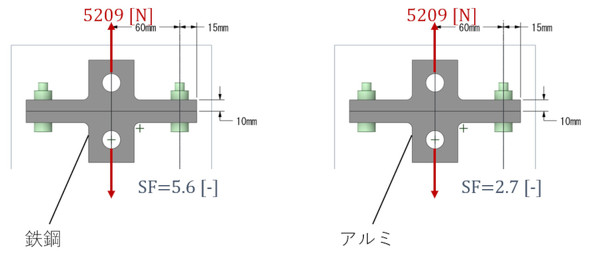
　例外に注目します。図12に示すように板厚が薄いとボルトが曲がりやすくなり、応力振幅が大きくなります。

図12　板厚が薄い場合［クリックで拡大］

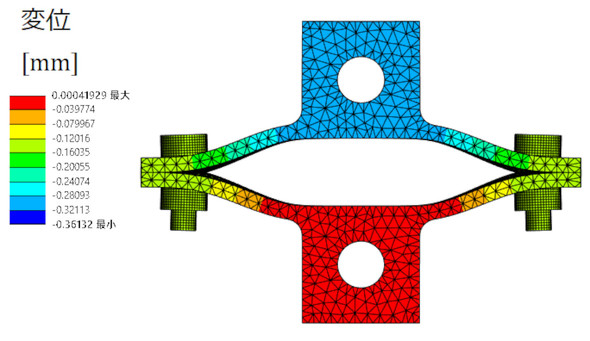
　応力振幅が大きくなった理由は、板厚が薄いので被締結体の剛性が低くなって、被締結体の変形が大きくなったためと考えられます。「剛性が低くなった」ということは、ヤング率の小さなアルミ材を被締結体とした場合は条件が悪くなると推測されます。図13に被締結体がアルミの場合の解析結果を示します。図13はサーベイした中で安全率が最も低かったケースです。

図13　被締結体がアルミの場合の解析結果［クリックで拡大］

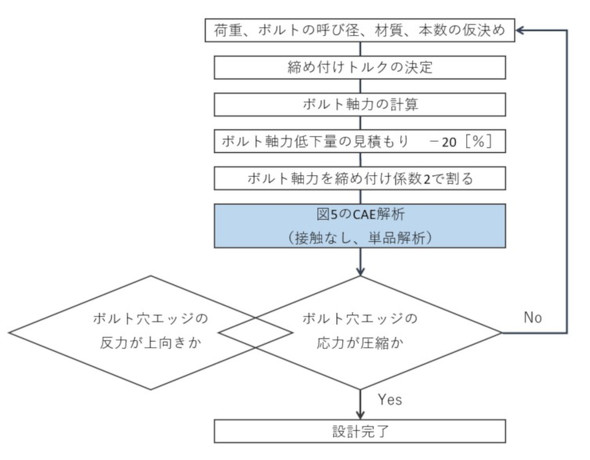
　安全率が下がりましたが2［-］以上となりました。被締結体がアルミの場合も同じ結論となり、例外も変わらない結果となりました。簡易的にボルトの疲労破断の有無を予測する手順を図14に示します。

図14　簡易的にボルトの疲労破断の有無を予測する手順［クリックで拡大］

　以上が、本連載で説明したかったことの全てです。