「ボルトの疲労強度」を理解する：CAEを正しく使い疲労強度計算と有機的につなげる（15）（3/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

ボルトの強度計算：解析モデル

　では、ボルトの疲労破断の有無の予測をしましょう。手計算ではなく有限要素法を使います。ボルトが2本以上あるときは有限要素法しか手段がないというのが筆者の主張です。理由は後述しますが、本連載の最後にフリーソフト「LISA」を使う方法を説明しますのでご安心ください。

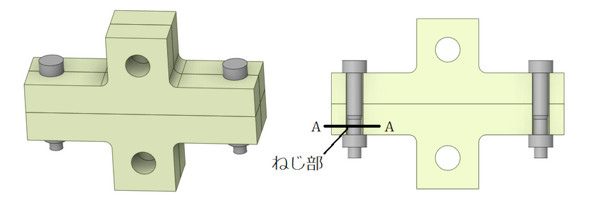
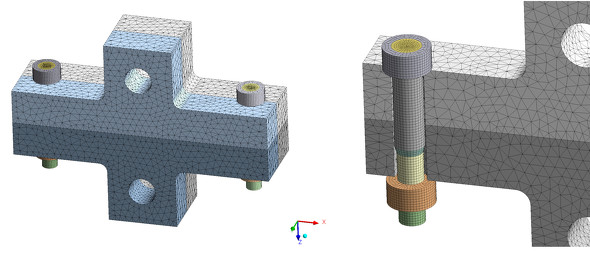
　図7に示すT形フランジを題材にします。表2に諸元を示します。ねじ部の直径は有効径d₂と谷径d₃の平均値です。図8に要素分割図を示します。

図7　解析モデル［クリックで拡大］

パラメータ	単位	値
T形フランジのヤング率	GPa	200
ボルトのヤング率	GPa	200
ねじの呼び	−	M10
締め付けトルク	Nm	78.0
摩擦係数	−	0.15
有効断面積	m2	5.95×10-5
軸力	N	38391
低下後の軸力	N	8188
ボルトの疲労強度	MPa	65
表2　T形フランジの諸元

図8　要素分割図［クリックで拡大］

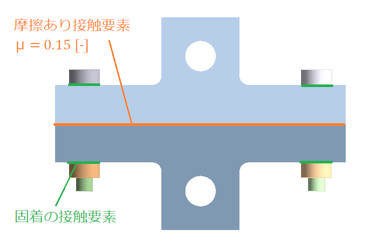
　図9に接触要素の配置位置を示します。被締結体の接触面は摩擦あり接触として分離可能としています。

図9　接触要素の配置［クリックで拡大］

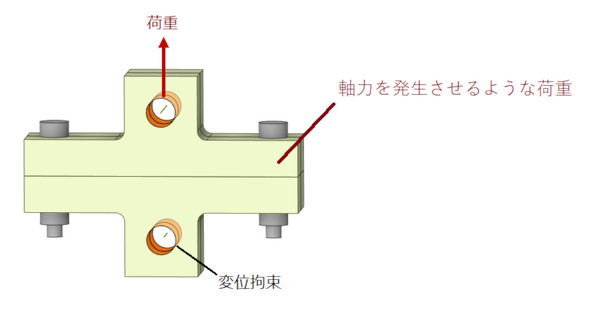
　図10に境界条件を示します。表3に示すように荷重は2段階に分けて印加します。内力係数による効果をシミュレーションで再現するためには、表3の「初期締結軸力を発生させるような荷重」は必須となります。今回は熱収縮を利用しますが、ボルトプリテンション機能が利用できるソフトもあります。軸力を発生させるような荷重のかけ方は次回で詳しく説明します。T形フランジへの荷重は、荷重ステップ1で「なし」、荷重ステップ2である値を印加します。

図10　境界条件［クリックで拡大］

	ボルトの荷重	T形フランジへの荷重
荷重ステップ1	初期締結軸力を発生させるような荷重	なし
荷重ステップ2	初期締結軸力を発生させるような荷重	印加
表3　荷重