「ボルトの疲労強度」を理解する:CAEを正しく使い疲労強度計算と有機的につなげる(15)(2/4 ページ)
ボルトの疲労強度:ボルト初期締結力を考慮
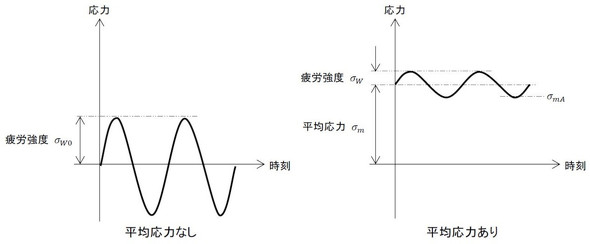
ボルトは決められたトルクで締め付けられているので、その軸力によって応力が発生しています。この軸力は平均応力となります。連載第7回で、平均応力が作用しているときの疲労強度は小さくなると述べました。平均応力が引張強さより少しだけ小さかったときのことを想像してみてください。小さな応力振幅で破断することになりますね。疲労強度が小さくなる様子を図5に再掲します。
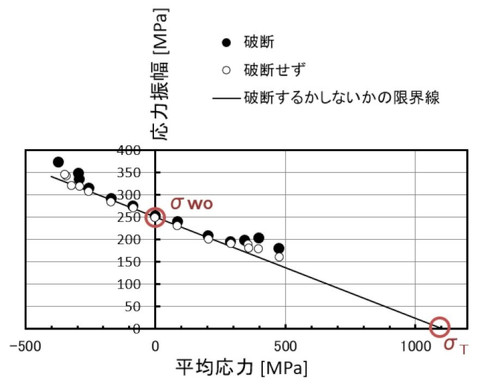
では、ボルトの場合の平均応力はどうかというと、図4から材料の降伏応力となります。図6に連載第7回で説明した疲労限度線図を再掲します。σTは真破断力でした。図6の破断するかしないかの限界線を式で表すと式1となります。
式1を切欠係数βで割ったものがボルトの疲労強度となり、式2です。
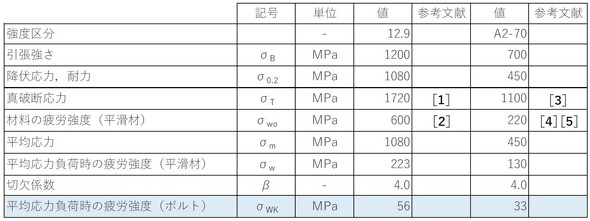
数値を代入しましょう。平均応力σmは、図4の結果から材料の降伏応力としました。強度区分12.9のボルトとステンレスボルト(A2-70)の疲労強度を表1に示します。強度区分12.9のボルトの疲労強度は56[MPa]となりました。参考文献[6]にはボルトの疲労強度が掲載されていますが、そこそこ一致していますし、ドイツのボルトの規格「VDI 2230 Blatt 1」による値と比較してもいい線いっています。
「切欠係数βはボルトの呼び径によらず4[-]で一定値、材料の疲労強度もボルトの呼び径によらず一定値」との仮定をしたので、ここで述べた方法ではどの呼び径でも同じ値となります。一方、参考文献[6]やVDI 2230 Blatt 1ではボルトの呼び径によって疲労強度が異なっており、細いボルトほど疲労強度が高くなっています。ここで述べた値はM24かM30に相当する値です。
表1の着色部で示した疲労強度は破断確率が50[%]なので、安全率を設定する必要があります。安全率を2[-]とすると、このときの信頼度は99.4[%]となります(参考文献[7])。つまり、破断確率は0.6[%]となります。
平均応力の考え方ですが、今回は降伏応力を採用しましたが公称応力で考えると降伏応力の70[%]となります。前者の方が疲労強度は低くなり、安全側の見積もりです。そして、前述した考え方による平均応力は図5のσmAに相当し、厳密な意味での平均応力ではありません。後の作業の煩雑さを考えてこのようにしました。厳密さを欠いた部分は安全率でカバーすることになります。
参考文献:
- [1]疲労強度の設計資料 I|日本機械学会(1988)
- [2]日本機械学会|機械工学便覧 A4 材料力学(1992)
- [3]渡辺、中村、福井、中西|SUS304ステンレス鋼のマルテンサイト変態を利用した磁気的傾斜機能材料|日本機械学会論文集 59巻 560号 P1138(1993)
- [4]竹内、松岡、西島、木村|室温におけるSUS304鋼の疲労特性|日本機械学会論文集(A編) 51巻 464号(S60)
- [5]林、榎本|オーステナイト系ステンレス鋼SUS304の高温大気中および高温純水中の疲労強度に及ぼす表面処理の影響|材料|Vol.45 No.10 P1107(1996)
- [6]吉本|ねじ締結体設計のポイント 改訂版|日本規格協会(2002)
- [7]山本|ねじ締結の原理と設計|養賢堂(2006)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

 式1
式1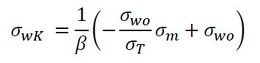 式2
式2