「ボルトの疲労強度」を理解する:CAEを正しく使い疲労強度計算と有機的につなげる(15)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第15回では「ボルトの疲労強度」について取り上げる。
» 2024年10月28日 09時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
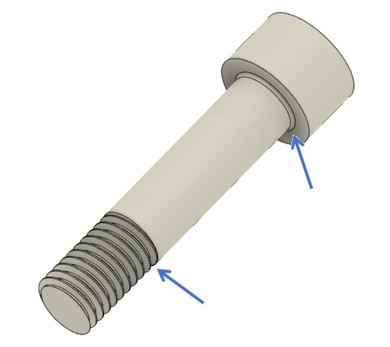
ボルトが疲労破断するとしたら図1に示した箇所です。そして、海外のボルトメーカーの方の話では「ボルトを曲げるような荷重が作用すると破断しやすい」とのことです。ボルトのねじ谷底は強烈な応力集中場なので、応力集中を考慮したボルトの疲労強度を求めましょう。
ボルトの疲労強度:ねじ山の谷底の応力集中の考慮
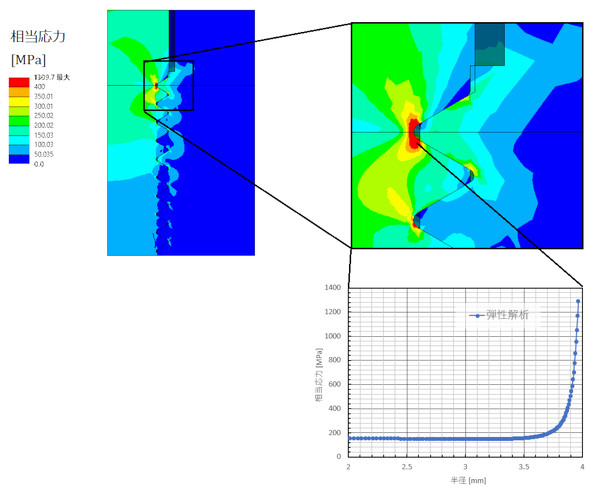
ボルトの締め付けトルクは、ねじ部の相当応力(応力集中を含まない公称応力です)が降伏応力の70[%]程度になるような大きさとするので、そのような荷重を与えたときのボルトの応力分布を図2に示します。ねじ山谷底には応力集中が発生していて、応力集中係数αは6[-]を超えています。
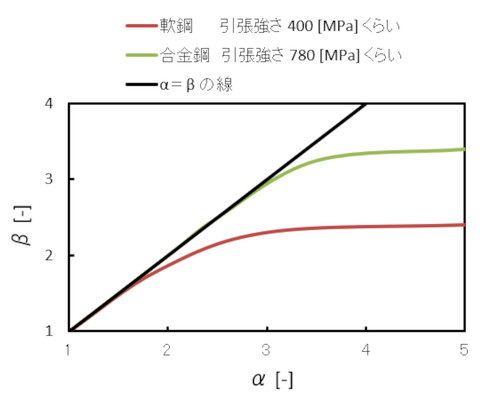
連載第8回で説明した応力集中係数αと切欠係数βの関係を図3に再掲します。合金鋼の場合、αがいくら大きくなってもβは3.4[-]くらいが上限です。引張強さがもっと大きなボルトを使うかもしれませんのでボルトのβは4[-]としましょう。
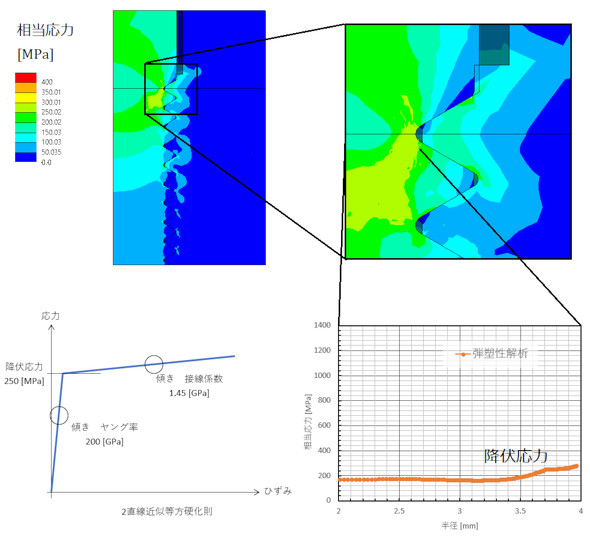
図2のねじ山谷底は、降伏応力を超えているので塑性変形します。材料を2直線近似当方硬化則として解析したものを図4に示します。応力は1300[MPa]になるのではなく250[MPa]ちょっと、つまり降伏応力+α程度ですね。
ねじ山の谷底は材料が降伏していますが、ねじ山の谷底の応力集中を考慮したボルトの疲労強度は、材料の疲労強度を前述したβで割った値となります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR