フローで考える流れのモデリング(その1) 〜流れの理論と流路網解析〜:1Dモデリングの勘所(29)(1/3 ページ)
「1Dモデリング」に関する連載。連載第29回では「フローで考える流れのモデリング(その1)」と題し、流れの理論と流路網解析について取り上げる。
モデリングの原点に立ち返り、物理量のフローをたどることにより、電気、熱、流れ、音振動といった現象を同じような手順でモデリングする方法の概要について前回紹介した。今回からは、この考え方に基づいて個別の現象への適用方法について説明する。今回は「フローで考える流れのモデリング(その1)」として、フローで考える流れの理論と流路網解析について取り上げる。
記事訂正のお詫び(編集部より):
記事内の一部の式に誤りがありましたため、お詫びして訂正させていただきます(修正箇所は赤字で示しております)。なお、流路網解析の事例は、正しい式で計算しているため図8の結果に誤りはございません。[更新2024年4月5日]
フローで考える流れの方程式
前回述べたように流れに関しては次式が成り立つ。前回と異なり、今回はより一般的な形式で表現している。これが通常表現と考えてほしい。
左辺第1項は慣性項、第2項は抵抗項、第3項は容量項で、Lを慣性要素、Rを抵抗要素、Cを容量要素と呼ぶことにする。右辺は圧力項である。上式を基に、流れに関する構成要素の一部(要素i、j)を抽出して表現すると図1となる。前回の図は容量項の片端がアースされているような図になっていたが、今回は誤解のないように実態に合わせて表記した。電気、熱、振動についても同様とする。ここで、要素iおよび要素jに流入する流量は流出する流量に等しい(電流則)ことより、
が、また圧力と流量の関係式(電圧則)により、
が成り立つ。ここで、要素iおよび要素jから外部への流れがないものとすると、未知数は圧力pi、pj、流量qiV、qij,qjVの5つで、上記の式の数(5つ)と一致するので解くことができる。実際には、n個の要素で構成されるより複雑な流れ系においても同様に解くことが可能だ。
流れに関する慣性要素と抵抗要素
流れの方程式の慣性項の慣性要素Lおよび抵抗項の抵抗要素Rの定義方法について考える。慣性要素Lおよび抵抗要素Rは、形状が存在しない構想設計段階では、その値自体を問題とするが、設計が進行するにつれて基本形状に当てはめて考える必要が生じる。基本形状の性質によって、その手順はさまざまであるが、ここでは一例として、図2に示すように、長さlの管があり、その断面積をA、管周長をs、両端の圧力をp1(上流側)、p2(下流側)、内部を流れる流体の速度をu、密度をρ、管壁面の剪断力をτとすると次式が成り立つ。
u=q/Aであるから、
となる。さらに、剪断力を速度変化に伴う損失の形式で表現すると、
となる。この右辺第1項が慣性項で、
となる。
一方、流路抵抗には大きく、摩擦による損失に起因するものと、速度変化による損失によるものに分類できるので、以下、この2つについて考える。
摩擦による損失:hf
管路壁面には、粘性による剪断応力が発生し、これが摩擦(friction)による圧力損失の原因となる。直径d,管路長lの圧力損失Δpは、比重量をγ、速度をuとして次式で表現できる。
λは管摩擦係数で、レイノルズ数ud/vと管壁の租度k/dで決定される。機能モデルでは形状が存在しないので、Δp=Rq|q|と表現した。管路の断面積をAとするとq=Auなので下記となる。
速度変化による損失:he
管路の断面積変化により、管内流速が変化することによって生じる圧力損失である。減速の際には、圧力上昇を伴うので、管壁面の境界層は剥離しやすく、剥離すると渦が発生し、流れのエネルギー損失が大きくなる。このような損失を「渦損失(eddy loss)」といい、次式で表現する。
ζは水頭損失係数で、レイノルズ数、管路断面形状によって変化するが、レイノルズ数の影響は小さいので通常無視される。また、速度uは、管路における速度のうち、早い方をとることが多い。摩擦の損失の場合と同様にして下記となる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
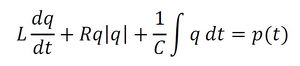 式1
式1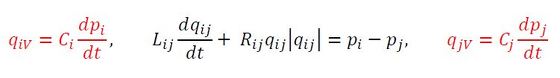 式3(初出時から訂正あり[赤字部分])
式3(初出時から訂正あり[赤字部分])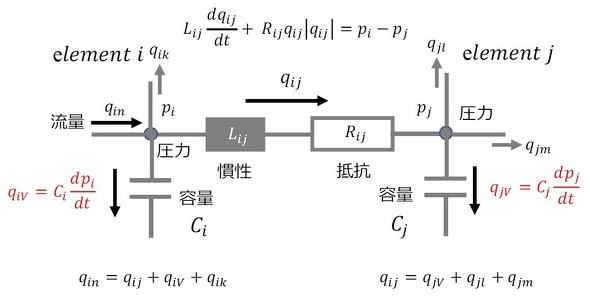
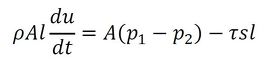 式4
式4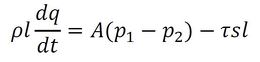 式5
式5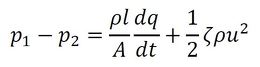 式6
式6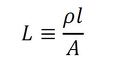 式7
式7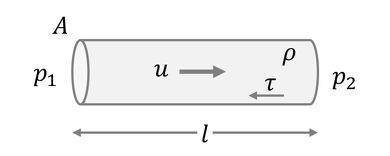
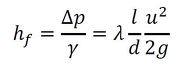 式8
式8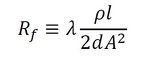 式9
式9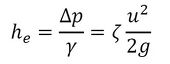 式10
式10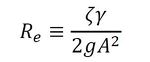 式11
式11





