フローで考える流れのモデリング(その1) 〜流れの理論と流路網解析〜:1Dモデリングの勘所(29)(2/3 ページ)
流れに関する容量要素の3形態
容量項について考える。容量項は流れの一部の体積変化により、流れの流量が変化することによって発生する。このようなパターンはいくつか存在する。ここでは3つのパターン、すなわち、空気だまり、大気開放タンク、流体の圧縮性・管の弾性について考える。
空気だまり:
図3に示すように、中央にタンクがあり、タンク上部には体積V、体積弾性率Kの空気層があり、タンクの下部(液層)両端は質量流量dm1/dt、dm2/dtを有する配管とつながっている。このとき、力の釣り合いおよび体積弾性率の定義式K=−V(dp/dV)から、
が成り立つ。dm1/dt=ρq1、dm2/dt=ρq2なので、上式は、
となる。この式を変形すると、
と容量項の式となり、これから容量要素は、
となる。今、等温変化を考えるとp∝1/Vであるから、K=pとなり、断熱変化を考えるとp∝1/Vγであるから、K=γpとなる。γは比熱比で1気圧、20℃の空気の場合、γ=1.402である。また、大気気圧はp=1.01325×105[Pa]である。
大気開放タンク:
図4に示す大気開放タンクを考える。タンクに流入流出する流量の差分に流体の密度ρおよび重力加速度gを乗じて、タンク断面積Aで除した値が圧力として作用する。すなわち、
となり、これから大気開放タンクの容量要素は、
となる。
流体の圧縮性・管の弾性:
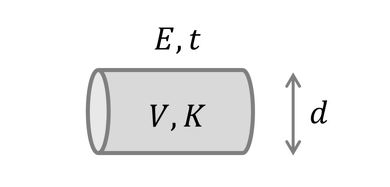
水も空気ほどではないが、圧縮性を有する。また、流体を包含する管も弾性を有している。このため、圧力を受けると流体が圧縮され、管が膨らむため、これを補う形で流量が増加する。従って、図5に示すように体積弾性率K、体積Vの流体(水)が直径d、肉厚t、縦弾性係数Eの管で覆われているとき、流量qと圧力pの間には次の式が成り立つ。
管の弾性の影響は、内圧pを受けると管の半径rはΔr=pr2/Etだけ伸びることより導出できる。以上から、流体の圧縮性・管の弾性を考慮した際の容量項の容量要素は、
となる。なお、常温常圧での水の圧縮率(体積弾性率の逆数)は1/K=0.485×10-9[Pa]である。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 幾何公差の基準「データム」を理解しよう
- 3σと不良品発生の確率を予測する「標準正規分布表」
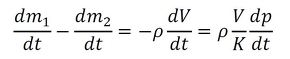 式12
式12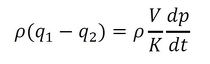 式13
式13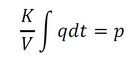 式14
式14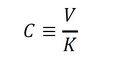 式15
式15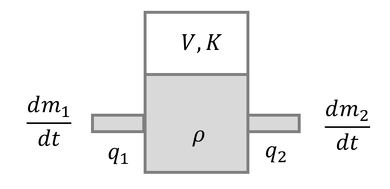
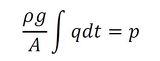 式16
式16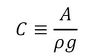 式17
式17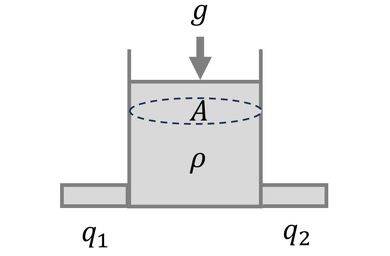
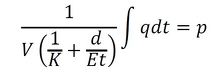 式18
式18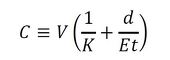 式19
式19