連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法:CAEを正しく使い疲労強度計算と有機的につなげる(2)(3/3 ページ)
2.全体剛性マトリクス 二次元平面応力
二次元問題とし、平面応力状態、つまり厚さ方向の応力がゼロの状態の三角形要素の要素剛性マトリクスを使って、各節点の変位を求める手順を説明しましょう。板厚が単位長さ(1[m]のことです)の板に荷重が作用し、変位した状態を図3に示します。
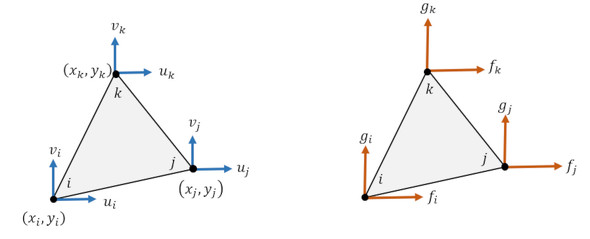
(xi,yi)、(xj,yj)、(xk,yk)は節点座標で、変位ベクトルと荷重ベクトルは次式で定義します。
剛性マトリクス[k]を次式で表現します。剛性マトリクスの各要素は材料のヤング率、ポアソン比と節点座標から求まりますが、これについては次回説明します。
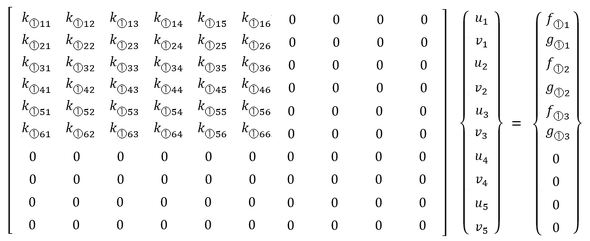
荷重と変位の関係は次式で表されます。
式20、式21は、6個の式からなる連立方程式とお考えください。
では、全体剛性マトリクスを作りましょう。図4に示すような3つの要素から構成される構造物をモデルにして説明します。要素番号は丸数字①②③で書くのがお約束です。表1に節点番号と要素番号の関係を示します。
| i節点 | j節点 | k節点 | |
|---|---|---|---|
| 要素① | 1 | 2 | 3 |
| 要素② | 2 | 4 | 3 |
| 要素③ | 3 | 4 | 5 |
| 表1 節点番号と要素番号の関係 | |||
節点1はx方向変位が拘束され、節点2はx方向とy方向の変位が拘束されています。そして、節点5にy方向の外力Wが作用しているとします。
要素①の荷重と変位の関係をマトリクス形式と連立方程式で表しましょう。
続いて、要素②の荷重と変位の関係もマトリクス形式と連立方程式で表しましょう。
要素①と要素②は節点2と節点3を共有しています。ということは、式22-3と式23-1を足し算できます。次式となります。
分かりづらくなったのでマトリクス表示しましょう。まず、式20を拡張して大きな器を作ります。
式22-3と式23-1を足し算して式24を作ったということは、マトリクス表示では以下となります。
では、式22-4と式23-2を足算、式22-5と式23-5を足算、式22-6と式23-6を足算して、式22-3と式23-4とはゼロに加算しましょう。以下となります。
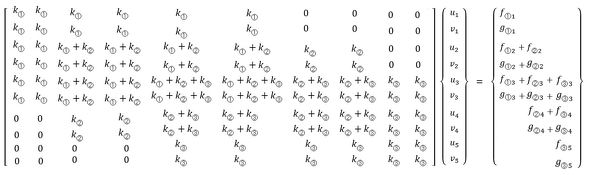
要素②と要素③は、節点3と節点4を共有しています。同様の操作をすると以下のような10行10列の剛性マトリクスと、10行の変位ベクトルの積が荷重ベクトルとなるマトリクス表示の連立方程式が出来上がります。
式28で全体剛性マトリクスができました。少し疲れましたね。今回はこの辺にしておきましょう。 (次回へ続く)
Profile
高橋 良一(たかはし りょういち)
RTデザインラボ 代表
1961年生まれ。技術士(機械部門)、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。
構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置(MRI装置)の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在RTデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ RTデザインラボ
関連記事
 疲労破壊が起きない条件を考える 〜ボルトの疲労強度〜
疲労破壊が起きない条件を考える 〜ボルトの疲労強度〜
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第2回は、疲労破壊の発生有無を予測する際に必要となる「ボルトの疲労強度」と「ボルトの締め付け条件」の検討のうち、ボルトの疲労強度の検討アプローチについて詳しく取り上げる。 ボルトが疲労破壊しない条件
ボルトが疲労破壊しない条件
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第3回は「ボルトが疲労破壊しない条件」について詳しく取り上げる。 設計者CAEによる締結部の設計法
設計者CAEによる締結部の設計法
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第7回では、本連載の最終目標である設計者が使うCAE環境で、必要とされるボルトの呼び径と本数を決める設計法を取り上げる。 疲労解析に挑戦、強度設計における繰り返し荷重を評価する
疲労解析に挑戦、強度設計における繰り返し荷重を評価する
初心者を対象に、ステップアップで「設計者CAE」の実践的なアプローチを学ぶ連載。詳細設計過程における解析事例を題材に、その解析内容と解析結果をどう判断し、設計パラメータに反映するかについて、流れに沿って解説する。第9回は、強度設計において、繰り返し荷重を評価する際に用いられる「疲労解析」を取り上げる。 固有振動数解析の流れを“ステップ・バイ・ステップ”で理解する
固有振動数解析の流れを“ステップ・バイ・ステップ”で理解する
「構造解析」を“設計をより良いものとするための道具”として捉え、実践活用に向けた第一歩を踏み出そう。第6回は「固有振動数解析」をテーマに取り上げ、その手順についてステップ・バイ・ステップで解説する。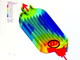 熱交換器の破断、熱流体と構造の連成解析で原因を同定
熱交換器の破断、熱流体と構造の連成解析で原因を同定
アルテア・エンジニアリングが2014年7月に開催した「2014 Japan Altairテクノロジーカンファレンス」で、住友精密工業 航空宇宙熱制御システム部 技術課の田谷亮氏が、航空機エンジンなどに使われる熱交換器に熱流体と構造の連成解析を適用した事例を紹介した。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

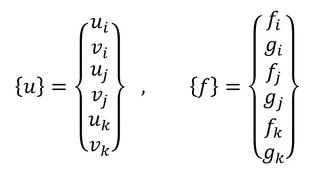 式18
式18 式19
式19 式20
式20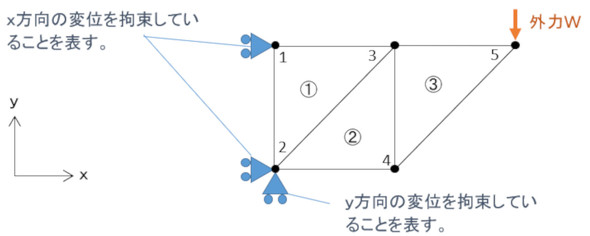
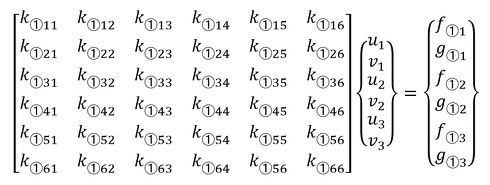 式22
式22 式23
式23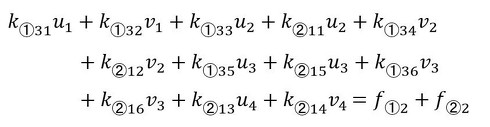 式24
式24