連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法:CAEを正しく使い疲労強度計算と有機的につなげる(2)(2/3 ページ)
1.要素剛性マトリクスの簡単な説明
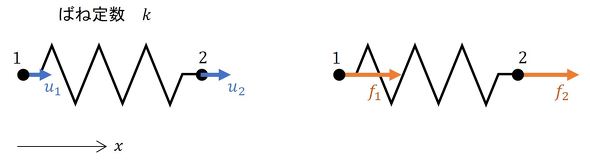
1本のばねで要素剛性マトリクスを説明します。図2のようなばねがあって、両端の変位をu1、u2とし、両端に作用する力をf1、f2とします。変位も荷重も右向きをプラスとします。
u1<u2の場合を考えましょう。ばねはu2−u1だけ伸びているので、ばねが縮もうとする力はk(u2−u1)となります。荷重の右向きをプラスとしたので、荷重は次式となります。
上式をマトリクス表示しましょう。次式となります。
上式では[k]を「要素剛性マトリクス」、{u}を「変位ベクトル」、{f}を「荷重ベクトル」と呼んで次式で定義しました。
では、連立方程式である式1、式2を解いてみましょう。行列式を使うとu1、u2は次式となるはずです。
|A|は行列式でした。次式で計算します。
では、式5の分母を計算しましょう。
分母がゼロとなってしまいu1、u2を求めることはできません。図2をよく見てみると、ばねの一端を固定していませんね。これではばねはx方向に自由に動いてしまいます。このような状態を「剛体変位」といいます。CAEソフトでは固定が十分でない場合に相当します。「ピボットがゼロになりました」というようなメッセージとともに異常終了するか、とても大きな変位を結果として出力します。
u1=0として、ばねの一端を固定しましょう。式1、式2は直ちに解くことができて、他端の変位は次式となります。
マトリクス表示した場合はどうでしょうか。やってみましょう。式3にu1=0を代入します。
式9について、変位が未知なものと既知なものを分けましょう。分割線を青線で描きます。
行列式の下半分を取り出します。
上式の左下Cのところはゼロとの掛け算なので、行列の下半分は次式に書き換えられます。
右下Dのところは、今回たまたま1行1列の行列でした。変位ベクトルと荷重ベクトルもたまたま1行でした。上式をマトリクス表示しましょう。
行列[k]の逆行列を式13の左側から掛け算しましょう。
外力f2が作用したときの変位u2が求まりました。
次に、式10の上半分を計算します。左上Aはゼロとの掛け算なので不要です。マトリクス表示で書きます。
固定点の反力が求まりました。以上の説明は、1行1列の行列を使ったので分かりにくかったかもしれませんが、ポイントは式10の行列を4つに分解するところです。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞

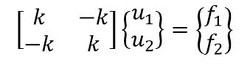 式3
式3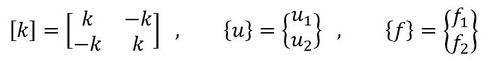 式4
式4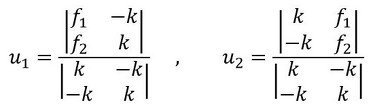 式5
式5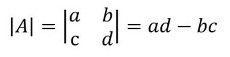 式6
式6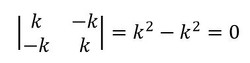 式7
式7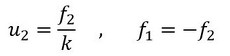 式8
式8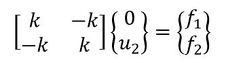 式9
式9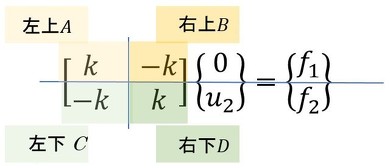 式10
式10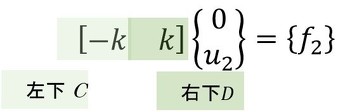 式11
式11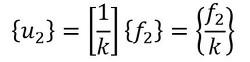 式15
式15





