振動形状をスローモーション表示してどこが変形しているかを確認する：CAEと計測技術を使った振動・騒音対策（14）（4/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

シミュレーションによる周波数応答解析

　紙面が余りましたので、シミュレーションによる周波数応答解析を紹介します。この解析からは伝達関数の大きさ（ゲイン）と位相が求まります。この計算に相当する実験行為は実験モーダル解析のところで述べました。

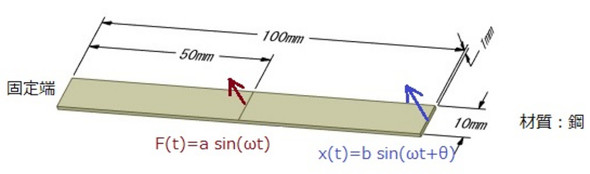
　図10に示すように、片持ちはりの中央（50［mm］のところ）に、sin波状に変化する力を加えたとします。

図10　周波数応答解析のモチーフ［クリックで拡大］

　片持ちはりは、最初は片持ちはり自身の固有振動数の振動と加えた力の周波数の振動の和の振動をしますが、前者は減衰し、いずれは加えた力の周波数の振動だけになります。周波数応答解析では後者の振幅と位相角を求めることができます。加える力の周波数はいくつも設定できるため、解析結果の振幅と位相は横軸を周波数としたグラフになります。力の振幅を1［N］とすれば、それは実験モーダル解析のところで求めた伝達関数となります。

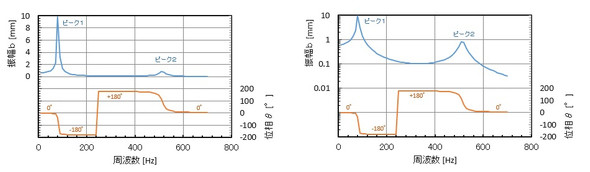
　周波数応答解析では、はりのどの点の応答（振幅bと位相角θ）も出力します。例えば、先端の応答ならば、それらをグラフにすると図11左図となります。2つ目のピーク、つまり2次の振動モードの振幅が小さくて分かりづらいため、図11右図のように振幅を対数表示にします。

図11　周波数応答解析の例［クリックで拡大］

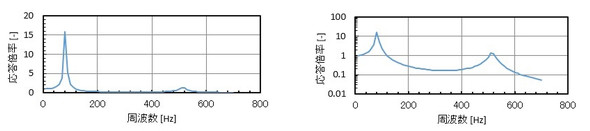
　周波数ゼロのときの振幅（静的変位）をb_staticとすると、振幅bをb_staticで割ったものを「応答倍率」や「動的応答倍率」と呼びます。b_staticは荷重をばね定数で割ったものですね。図12のように応答倍率をグラフで表したものを「共振曲線」や「変位共振曲線」と呼びます。

図12　応答倍率［クリックで拡大］

　ピークでの振幅は共振状態の振幅であり、減衰に関する数値を与えないと有限要素法ソフトはとても大きなでたらめな値を出力します。減衰がゼロで、かつ線形解析であるため、理屈上の振幅は無限大です。共振点近傍の振幅を求めたい場合は、正確な減衰定数を入力する必要がありますが、以前お話したように減衰定数は物質固有の値ではなくて、いくつかの部品が組み合わさった構造物の部品間の接触状態やその他の要因で決まるものなので、シミュレーションを始める時点でこれを正しく把握することはなかなかできません。通常は「今回は応答倍率を10［-］くらいとして計算してみましょうか」などの会話の後、計算することになります。

　共振点の振幅を求めることはまれで、普通は加振源の周波数の振幅（共振点近傍の山の裾野の振幅）を求めることが多いので、前述した減衰に関する問題はそれほど深刻にはなりません。

---

　さすがに勤めていた当時のデータを使うわけにはいかないので、今回のアニメーションは作った値ですが、かなり実際と近いものができました。これまで解説してきた内容で機械の性能向上が図れると思いますが、次は“機械の性能向上に特化した内容”を紹介することにします。　（次回へ続く）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ