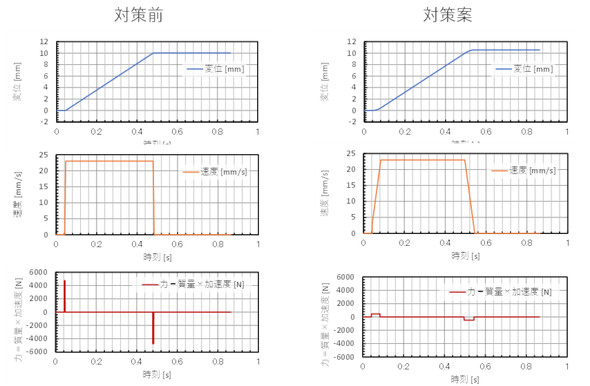
　対策として、モーターの駆動方法を変えてみましょう。ソフトの設定値を変えるだけなのでコストはかかりません。図5の速度波形を見ると、急加速、急減速しています。加速の度合いを小さくしてみます。図9に変位、速度、力の波形を示します。力の大きさは0.10倍ですが、力が作用している時間は10倍に長くなっています。振動は0.10倍になるでしょうか。

図9　モーター駆動パターンの変更［クリックで拡大］

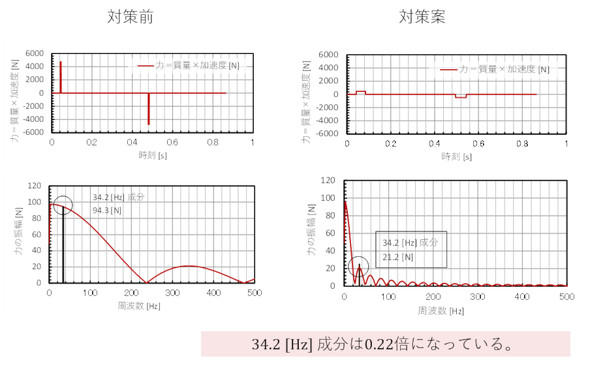
　図10に、力の周波数分析を示します。力の高周波成分が低減し、34.2［Hz］成分は0.22倍になっています。

図10　力の周波数分析［クリックで拡大］

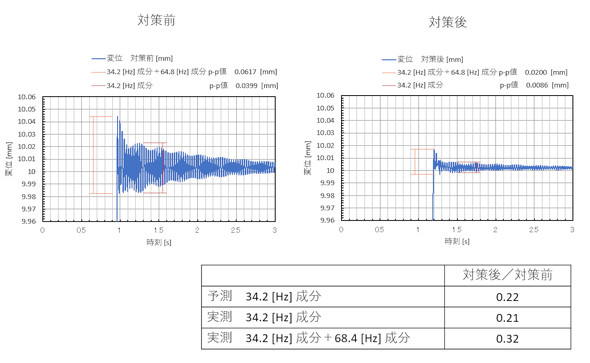
　図11に、対策前後の振動変位を示します。34.2［Hz］成分は0.21倍となり図10の予測と一致しましたが、68.4［Hz］成分を含めると振動変位は0.32倍と約3分の1になりました。

図11　対策前後の振動変位［クリックで拡大］

　以上のように、振動量や加振力について、横軸を周波数として捉え、伝達関数を求めると、対策立案が容易となり、対策効果を予測することができます。

生産機械の場合

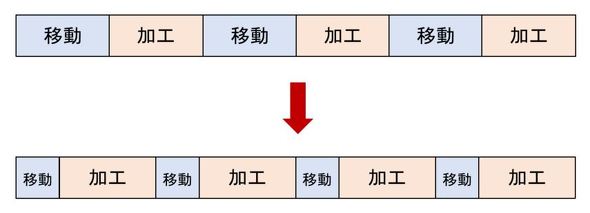
　ここで紹介した内容は、簡単な例でした。動作が悠長というか、加速と減速に要する時間をまだまだ長くすることができましたが、このように時間を伸ばせることができない機械も多くあります。通常、生産機械は単位時間当たりの生産数を最大限にするように要求されています。多くの場合は、ワークの移動と加工の繰り返しです。図で表すと図12のようになるでしょうか。移動時間は価値を生み出していないので短くしなければなりません。図のように移動時間を短くすると、3個生産できたものが4個生産できるようになります。

図12　生産機械の動作パターン［クリックで拡大］

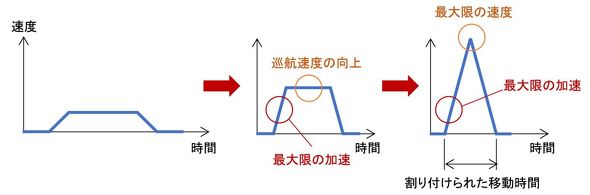
　このような事情から移動速度は最大限に上昇します。図13に、生産数増加のための速度パターンの変化を示します。図13左図のような悠長な速度パターンは許されず、図13中央図のように加速を最大限にし、巡航速度を増加します。そして、さらなる時間短縮のためには、既に加速は最大限になっているので、図13右図のような三角形の速度パターンとなります。

　この三角形速度プロファイルは案外「あるあるプロファイル」です。このような場合は前述した力の高周波成分を低減させる作戦は使えず、装置のメカ設計を変える必要が生じます。