振動対策のアプローチについて考える:CAEと計測技術を使った振動・騒音対策(7)(2/4 ページ)
伝達関数で対策を考えよう
振動対策の次の手は「伝達関数」の推定です。伝達関数をおさらいします。あるシステムがあって、そのシステムの入力を時間の関数として、f(t)とします。今回の場合は力です。入力は力であることが多いので、f(t)と表記しました。システムの出力も時間の関数としてx(t)とします。今回の場合は、XYテーブルの変位から振動成分だけを取り出したものとしましょう。入力と出力をラプラス変換して、出力を入力で割ったものが伝達関数です。次式となります。図で表すと図6となります。
sの代わりにjωを代入したものが「周波数伝達関数」です。次式となります。ωは角振動数で、fを周波数とすると、ω=2πfです。式6に示した周波数伝達関数の位相の式ですが、正確にはアークタンジェントではなく位相角が−180[deg]〜180[deg]となるようにしなければならず、ちょっとしたプログラムが必要です。配布したマクロ付きExcelファイルの関数「fft_ang( )」のプログラムリストを参照してください。
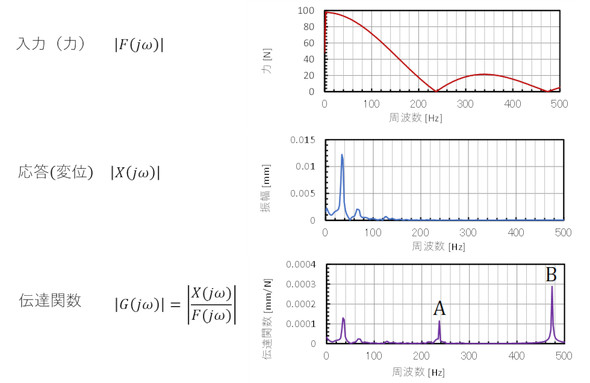
本連載の振動/騒音対策では、ラプラス変換の計算はしません。式3の|G(jω)|と∠G(jω)を実験的に求めます。∠G(jω)は実験モーダル解析のところだけ登場します。では、|G(jω)|を求めましょう。図3の振動波形の周波数分析を、図5の力の周波数分析で割り算すれば、この装置の周波数伝達関数の絶対値が求まります。図7に示します。図のAとBのピークには注意が必要です。分母である|F(jω)|がこの周波数ではゼロなので、ゼロによる割り算をしています。このピークは無視しなければなりません。
市販のFFTアナライザの入力は2チャンネルあり、伝達関数を直接求めることができるようになっています。測定データをExcelに取り込めれば、FFTアナライザがなくてもできますね。式5を変形します。応答は次式となります。
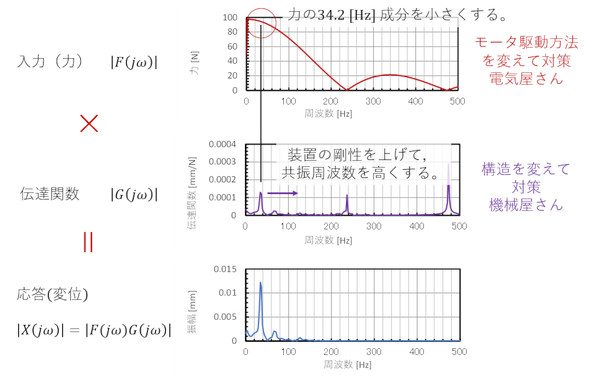
応答は、伝達関数と入力の積ですね。図で表すと図8のようになります。振動低減には、「(1)入力を変える」手段と「(2)伝達関数を変える」手段があります。入力を変えるときは、モーターの駆動方法を変えて、力の34.2[Hz]成分を小さくすればよいことになり、電気屋さんか制御屋さんの仕事になります。伝達関数を変えるときは、装置の剛性を上げて「共振周波数(固有振動数)」を高周波側にシフトすればよいことになり、機械屋さんの仕事です。伝達関数で現象を把握すると、対策案が1つではなくいくつか出てきて、それら対策案のうちどの案のコスパが良いかを比較することもできます。
過去の話ですが、電気屋さんと機械屋さんはたいがい仲が悪く、「お前がやれよ!」といった感じで、仕事の擦り付け合いが始まるのでした……。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

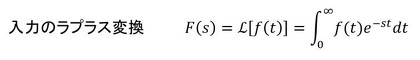 式1
式1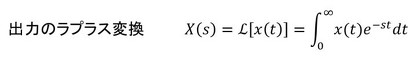 式2
式2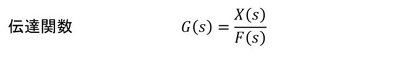 式3
式3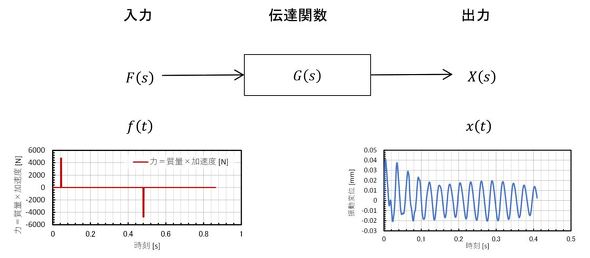
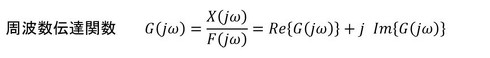 式4
式4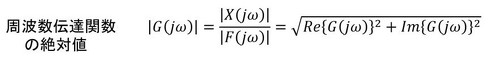 式5
式5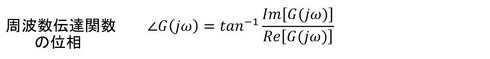 式6
式6