疲労破壊が起きない条件を考える 〜ボルトの疲労強度〜:設計者向けCAEを使ったボルト締結部の設計(2)(2/4 ページ)
ボルトの疲労強度の文献値
疲労破壊の検討には、“ボルトの疲労限度”を求める必要があります。ステンレス鋼を除く鉄鋼材料には、S-N曲線において実験値を線で結ぶと、繰り返し荷重回数が106〜107回のところから水平になる現象が起こりますが、この応力振幅を「疲労限度」といいます。この応力以下では、無限回の繰り返し荷重に耐えられると考えられています。ステンレス鋼やアルミニウム材は疲労限度が現れず、荷重回数が107回くらいのところの応力振幅を疲労限度とすることが多いようです。無限回の荷重には耐えられませんので、以降、本連載では「疲労限度」とは呼ばずに「疲労強度」と呼ぶことで統一します。
ボルトの疲労強度の推定値σWKの文献値を比較してみましょう。この数値は公称応力、つまり、ねじ谷底の応力集中を考えずに、荷重振幅を有効断面積で割った値です。有効断面積の代わりに谷径による断面積を使った文献もありますが、本連載では有効断面積を使います。
参考文献[1]によると、疲れ限度の推定値σWKはM12・強度区分12.9で約40[MPa]です。参考文献[2]によると疲労強度の許容値として式1を採用しています。
これは「VDI 2230, Blatt 1(1986)」から引用されており、破壊確率が1%における値で、強度区分8.8〜12.9に限定されています。M24・強度区分12.9の場合、47[MPa]ですが、これには安全率が含まれています。
参考文献[3][4]によると、疲れ限度の推定値σWKはM24・強度区分8.8で43[MPa]、強度区分12.9で61[MPa]です。
なぜ、M24の値だけを示したのかというと、呼び径がM24よりも小さなボルトの疲労強度はこれよりも大きな値になるため、M24よりも小さな呼び径のボルトを採用する設計の場合、M24の値を採用しておけば安全側の設計になるからです。
そして、それぞれの参考文献で共通していえることは、
- 平均応力、つまりボルトによる締め付け力が変わっても一定値である
- 強度区分4.8と12.9で疲労強度は3倍の差があるのではなく、例えば、M24においてはその差は2倍以下である
- 呼び径が大きくなると疲労強度は減少するが、M16以上では減少度合いが緩慢となる
ということです。
ボルトの疲労強度は、強度区分12.9で40〜60[MPa]の範囲にあり、強度区分12.9の引張強さは1200[MPa]なので、引張強さの約24分の1ととても小さくなっています。
参考文献:
- [1]:山本晃:ねじ締結の原理と設計:養賢堂(2004)
- [2]:酒井智次:増補 ねじ締結概論:養賢堂(2008)
- [3]:吉本勇:ねじ締結体設計のポイント:日本規格協会(2002)
- [4]:吉本勇:ねじの疲れ強さに関する一仮説:精密機械,49巻6号 P801(1983)
ボルトの疲労強度を求めてみよう(1)
前述の参考文献の値を採用してもいいのですが、ここでは強度区分12.9のボルトと強度区分A2-70のステンレスボルトの疲労強度を自分で求めてみましょう。
強度区分12.9のボルトの引張強さは1200[MPa]、0.2%耐力は1080[MPa]です。平滑材(切り欠きのない材料)の疲労強度は、参考文献[5]に非常に多くの実験値をプロットした図が記載されており、“引張強さの0.5倍”と考えてよさそうです。引張強さが大きな材料は0.5倍という数字が小さくなる傾向にありますが、1200[MPa]程度なら0.5倍でいいと思います。よって、疲労強度は600[MPa]となります。ただし、この値は両振り荷重(交番荷重)での値であり、かつマージンが含まれておらず、破壊確率が50%だと考えるべきです。
参考文献:
- [5]:日本機械学会:機械工学便覧 A4 材料力学 P117(1992)
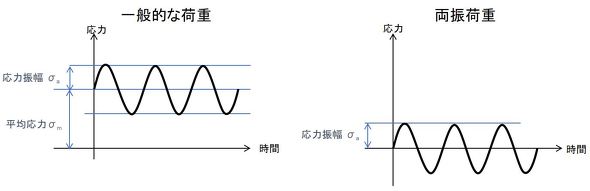
一般的な変動荷重が作用するときの応力を図8に示します。平均応力と応力振幅があります。両振り荷重というのは平均応力がゼロの場合です。平均応力が大きくなった場合を考えましょう。平均応力が引張強さに到達したときは、応力振幅がなくても破壊が生じます。平均応力が引張強さよりも少しだけ小さいときは、とても小さな平均応力で疲労破壊すると考えられます。つまり、疲労強度(疲労破壊しない応力振幅)は、平均応力が大きいほど小さくなります。ここで、応力の符号について触れておきます。プラス(+)の応力は引張応力、マイナス(−)の応力は圧縮応力だということはお約束です。
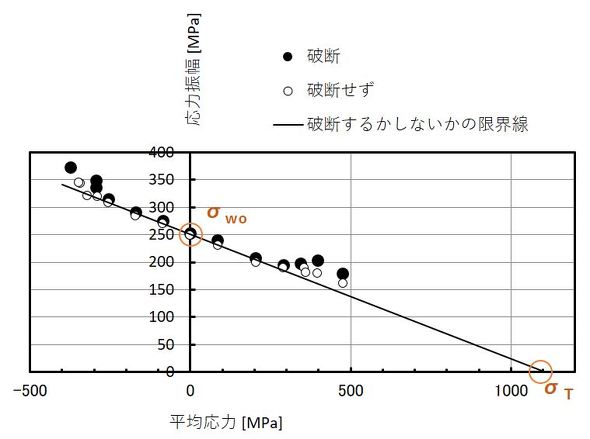
平均応力が大きくなると、疲労破壊しない応力振幅はどのように減少していくのでしょうか。日本で初めて「疲労限度線図」を紹介したと推測される参考文献[6]のデータを使って説明します。試料は炭素濃度が0.4%Cの炭素鋼で、引張強さσBは696[MPa]、降伏応力σyは382[MPa]、両振り疲労強度σwoは251[MPa]、真破壊応力σT(引張試験で試験片が破壊したときの荷重を破壊後の断面積で割った値)は1107[MPa]でした。
図9は平均応力を変化させて疲労強度を調べた結果で、参考文献[6]の数値を読み取りプロットしました。黒色丸印のプロット(●)が破断したデータ、白色丸印のプロット(○)が破断しなかったデータです。●プロットと○プロットの中間を結んだ線が疲労破壊が起こるか起こらないかの限界線で、1本の直線になります。この限界線は、平均応力が大きくなるにつれて疲労強度が低下することを示しています。実験データからこの限界線は、横軸(平均応力の軸)の切片を真破壊応力σTとし、縦軸(応力振幅の軸)の切片を両振り疲労限度σwoとした直線と一致します。縦軸を応力振幅、横軸を平均応力として、この限界線を描いた図を疲労限度線図といいます。
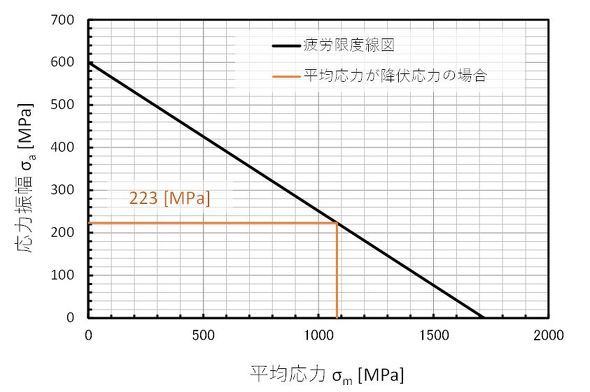
では、この疲労限度線図を使っていきましょう。強度区分12.9のボルトの疲労強度は600[MPa]でした。強度区分12.9のボルトは「SCMボルト」とも呼ばれる、黒色(黒色酸化被膜)のボルトです。真破壊応力σTは参考文献[7]から1720[MPa]となります。疲労限度線図を描いてみると図10のようになります。「ボルトの谷底はもう降伏している」で述べたように、平均応力は材料の耐力1080[MPa]とします。その結果、疲労強度は223[MPa]まで減少しました。
次に、谷底の応力集中による疲労強度の低下を考慮しなければなりません。切り欠き係数βについて考察します。
参考文献:
- [7]:日本機械学会:金属材料 疲労強度の設計資料 I(S63)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 製造業の情報を一元管理するDXプラットフォームの体験型施設を開設
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 幾何公差の基準「データム」を理解しよう
- 強度設計の出発点 “計算”より先に考えるべきこととは?
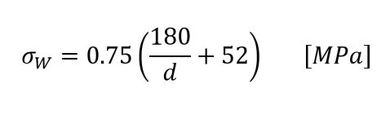 式1
式1