疲労破壊が起きない条件を考える 〜ボルトの疲労強度〜:設計者向けCAEを使ったボルト締結部の設計(2)(3/4 ページ)
ボルトの切り欠き係数βについて考察する
ボルトの谷底は、激しい応力集中を起こしているので疲労強度は減少します。ここでは、切り欠き係数βを導入します。
まずは、応力集中係数α(「形状係数」ともいう)と切り欠き係数βの定義をおさらいしておきましょう。αとβは次式(式2、式3)で定義されます(参考文献[7])。
αは形状だけで決まります。αが大きければβも大きくなることは自然な発想ですが、両者は一致しません。βはαと材料によって決まります。後述しますが、αが小さいときのβはαにほぼ等しく、αが大きくなると“α>β”となります。また“α>β”の領域では、βは材料の引張強さに依存し、引張強さが大きいほどβは大きくなります。
例えば、参考文献[1]では、参考文献[7]による両振り引張圧縮を受ける単一環状V溝付き丸棒に対する実験式に修正を加えてβを求めています。ちなみに、いまいちピンとこない単一環状V溝付き丸棒ですが、図11のような形状をしています。記号の意味は割愛しますが、この実験式は式4になります。
この方法によるβは強度区分4.8、M6ボルトで2.25、強度区分12.9、M24ボルトで10.8となります。
次に、参考文献[3]ではβを求めるのに、「石橋の疲れ破壊に関する説」(参考文献[8])を使用しています。この説は多くの論文で採用されており、これに従っていれば間違いないと思います。
参考文献:
- [8]:石橋正:金属の疲労と破壊の防止:養賢堂(1967)
少し説明しましょう。参考文献[3]によると、βは式5で表されます。
χはねじ谷底の最大応力勾配で、式6で定義されます。
σmaxは切り欠き底(谷底に相当します)の最大応力、sは最大応力勾配の方向に取った座標、dσ/dsは応力勾配です。σmaxと応力勾配は図7などから求めることができます。εoは結晶粒の大きさに影響を受ける定数とのことです。
参考文献[8]では、少し形が違っていて式7となります。
χとa1は同じで、ρは切り欠き半径です。εoは深い意味を持っていて説明が難しく、やたらなことを書いたら多くの研究者に「それは違う」といわれてしまいそうです……。参考文献[8]によると、
切り欠き底の応力ではなく、切り欠き底からεoだけ離れた点の応力が疲労限に達したらき裂が発生する
とのことです。ここには、結晶粒に関する記述はありません。
a1、εoはプラスの値を持つので、βはαよりも小さくなります。切り欠き感受性の考え方から、材料の引張強さが大きくなるほどβが大きくなるので、εoは材料固有の値と捉えればよさそうです。つまり、引張強さが大きくなるほどεoは小さな値を持つことになります。しかし、参考文献[8]には「αの影響を受けるかも」とも書いてあります。加えて、応力勾配が高いとβは小さくなることもこの式で表現することができます。
εoは何mmでしょうか。εoを測る物差しはありません。結晶粒の大きさがヒントになるのかもしれませんが決定的なものはなさそうです。εoの活用法として未知のβの推定があります。αと応力勾配を机上で求め、βを実験で得て逆算してεoを算出します。そして、未知のβに対しては先ほど求めたεoを使って予測します。
少し話が長くなりましたが、参考文献[3]ではεoからβを求めており、強度区分4.8、M6ボルト、谷底丸みが0.144×ピッチの場合で1.49、強度区分10.9、M24ボルト、同じ谷底丸みで4.37となります。
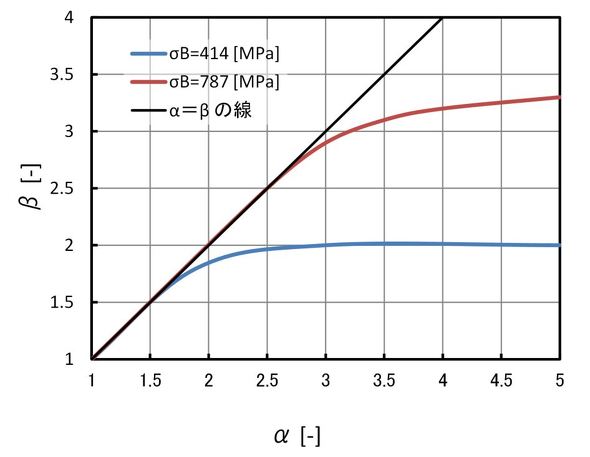
う〜ん。どうもしっくりときませんね。参考文献[7][8]を参考にして、自分で描き直したαとβの関係を図12に示します。
βがαを上回ることはなく常にα≧βで、小さいαの場合はα≒βとなります。大きなαの場合、αがいくら大きくなってもβは上昇せず一定値になります。βが4を超えることはなさそうです。参考文献[7]は、日本機械学会が多くの論文、文献から集めた疲労強度の集大成で、βに関して豊富な情報が載っています。さすがに参考文献[7]の図をそのまま掲載するわけにはいかないので文章で説明すると、横軸にβ、縦軸に疲労強度と引張強さの比をとって、今まで集めたデータを全てプロットしてあります。そのプロットを見ると、β>3のプロットは100個に1個くらいで、β>4のプロットはありません。つまり、βが4より大きいデータは観測されたことがないのです。
というわけで、βの上限値は4であるとするのが適当かと思います。βの下限値については、1〜2の値が示されているボルトの文献がありますが、どのようなボルト径でも谷底は降伏しているのです。降伏するような厳しい応力集中場で3より小さいβの採用は、心配性な筆者にとって受け入れがたいものです。以上のことから、ここでは「β=4」として検討を進めていきましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
 式2
式2 式3
式3
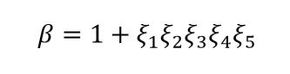 式4
式4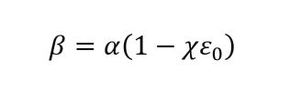 式5
式5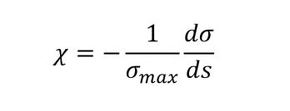 式6
式6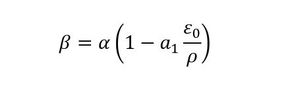 式7
式7