流れの計算に大きな影響を与える「レイノルズ数」を考える:初心者のための流体解析入門(4)(2/2 ページ)
世の中の多くのものは「ほぼ乱流」である
とはいえ、実際には世の中の多くのもの、すなわち私たちが日常的に解析の対象とするものは、ほぼ乱流であると考えて構いません。それは、ちょっと計算して見れば分かることです。
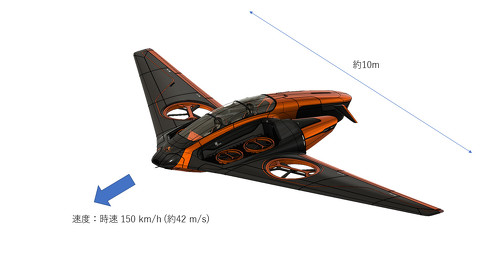
例えば、飛行機を考えてみましょう。それもジェット旅客機のようなスピードの速い飛行機ではなくて、最近注目を浴びてきている「アーバンエアモビリティ」を考えてみます。以下に示したのは、法政大学 アーバンエアモビリティ研究所のコンセプトモデル「Stingray」です(図1)。
翼端間の距離を10程度、巡航速度を約80ノットとすると、150km/h弱(約42m/s)くらいでしょうか。一般的な空気の場合、密度が1.206kg/m3、粘性係数が、1.83×10-5Pa・sです。これらの数値を基に、レイノルズ数を計算すると以下のようになります(式2)。
飛行機のような外部流れの解析では、数十万オーダー以上は乱流と考えられるので、この場合も乱流と考えられます。自動車でも代表速度と代表長さがこの数分の1程度なので、やはり乱流と考えられます。現実の物体を考えると、よほど小さなモデルや低速の状態でなければ、ほとんどの場合、乱流になると考えてよいでしょう。
では、内部流れはどうでしょうか? 例えば、水道管の水の流れを考えてみましょう(図2)。
家庭用水道管の口径は13mmか20mmですが、ここでは最近一般的な20mmを考えてみます。水の流速は2m/s程度だとします。ちなみに、水の密度は998.2kg/m3、粘性係数は0.001016Pas・sとします。これらを基にレイノルズ数を計算すると以下のようになります(式3)。
内部流れの場合、層流になるためにはレイノルズ数が数千オーダー必要なので、このケースも乱流となります。
つまり、一般的に私たちが扱う問題は「ほぼ乱流である」と考えて問題ないでしょう。ということで、今回はレイノルズ数が流体解析に与える影響の大きさについて解説しました。 (次回に続く)
Profile
水野 操(みずの みさお)
1967年生まれ。mfabrica合同会社 社長。ニコラデザイン・アンド・テクノロジー代表取締役。3D-GAN理事。外資系大手PLMベンダーやコンサルティングファームにて3次元CADやCAE、エンタープライズPDMの導入に携わった他、プロダクトマーケティングやビジネスデベロップメントに従事。2004年11月にニコラデザイン・アンド・テクノロジーを起業し、オリジナルブランドの製品を展開。2016年に新たにmfabrica合同会社を設立し、3D CADやCAE、3Dプリンタ関連事業、製品開発、新規事業支援のサービスを積極的に推進している。著書に著書に『絵ときでわかる3次元CADの本』(日刊工業新聞社刊)などがある。
関連記事
 設計者CAEとは何なのか
設計者CAEとは何なのか
機械メーカーで3次元CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は設計者CAEについて考える。 材力とFEMをシッカリ理解して、シッカリ解析!
材力とFEMをシッカリ理解して、シッカリ解析!
小難しい有限要素法を数式を使わずに解説する。まずは有限要素法の歴史を振り返り、解析の基本的な考え方を確認。 流体解析を行う上で必要なこととは? 【その1】解析領域
流体解析を行う上で必要なこととは? 【その1】解析領域
流体解析をテーマに、入門者や初学者でも分かりやすくをモットーに、その基礎を詳しく解説する連載。今回は“流体解析を行う上で必要なこと”として、解析領域について取り上げる。また記事後半では、流体解析ソフトウェアを用いた簡単な作業の流れについても紹介する。 【オリエンテーション】ハードルの高い流体解析だが設計現場でも少しずつ身近に
【オリエンテーション】ハードルの高い流体解析だが設計現場でも少しずつ身近に
解析、あるいはシミュレーションは、少なくともツールとしては、それほど特別なものではなくなってきた昨今である。特に設計者向けの構造解析については顕著である。しかし、流体解析についてはどうだろうか。 構造解析メインだったSIMULIA、ついに流体と電磁界へ
構造解析メインだったSIMULIA、ついに流体と電磁界へ
ダッソー・システムズ(以下、ダッソー)は2018年10月1日、同社のCAEシステム「SIMULIA」に関する記者発表会を開催した。2016〜2018年にかけて買収したCAE技術とSIMULIAの統合、同社のクラウド基盤「3DEXPERIENCEプラットフォーム」との連携に関する進捗について説明した。 かつてCAEを軽く見ていた設計者がその必要性について説く
かつてCAEを軽く見ていた設計者がその必要性について説く
かつて2次元大好き信者だった筆者が“CAEの重要性”に気が付いた経緯を踏まえつつ、話題の「設計者CAE」の基本的な考え方について解説する連載。第1回は、CAEの基礎として、その役割やメリットを紹介するとともに、設計者CAEを実践することで得られる効果について取り上げる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

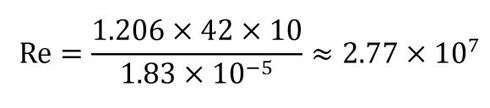 式2 アーバンエアモビリティ「Stingray」を題材にレイノルズ数を計算
式2 アーバンエアモビリティ「Stingray」を題材にレイノルズ数を計算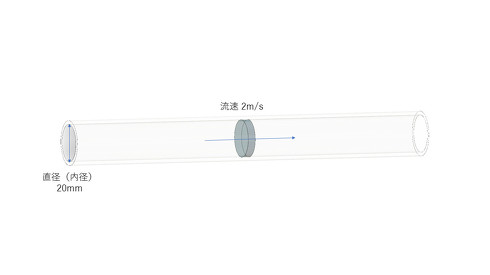
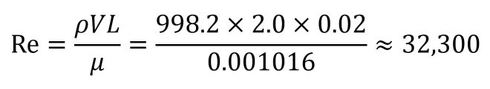 式3 水道管の水の流れを題材にレイノルズ数を計算
式3 水道管の水の流れを題材にレイノルズ数を計算






