走行距離不安症の数学:SYSTEM DESIGN JOURNAL(3/4 ページ)
複雑なアルゴリズム
こうした状況を見て、「これは隠れ状態を持つシステムなのだ」と考える設計者もいます。そうしたシステムを正確にモデル化でき、そのモデルによって、たとえノイズが多く信頼できない予測でも、外部から測定可能な状態から隠れた状態を予測することが可能な場合、隠れた変数を推定する既知の手法があります。この場合、セル温度、電圧、負荷電流などの値に基づいて充電状態を推定するということです。その手法とはカルマン・フィルターです。
カルマン・フィルターは、統計的管理理論家らに愛され、多くの技術者たちから恐れられている反復デジタル計算で、仮定が満たされた場合、外部から測定可能な状態変数を繰り返しサンプリングすることにより、システム内部の隠れ状態を正確に追跡することが可能です。
最大の利点はシステム状態の測定と知識の両方に大きなノイズが存在していても機能することであり、航空機誘導システムからスマートビークルのセンサーフュージョン、ブラシレスモーターのシャフト位置推定に至るまで、一見共通性のない幅広いアプリケーションに広く利用されています。もちろん、リチウム・バッテリーの充電状態の推定にも使用されています。
カルマン・フィルターは、推定対象のシステムのモデルから始まります。このモデルは、その時点(時間 t とします)におけるシステムの状態変数を、直前のサンプル時間 t-1 における状態変数と制御入力変数に単純なガウス・ノイズを加えた線形結合として表します。カルマン・フィルターが数学的に分かりにくい理由の1つは、ノイズの追加により、状態変数がスカラでなく、ガウス確率関数となることです。そのため、数学者は共分散行列について詳細に扱うことができ、ほとんどの場合、本当に注意を払うべきことは確率分布の平均だけです。
モデルの大きな重要性は、測定可能な変数と測定不能な変数の間に関係を生み出すことです。そのため、前のサイクルで観測可能な挙動に基づいて、システム内部の隠れ状態を予測します。当然ですが、カルマン・フィルターがノイズや不確かさの影響を受けずにうまく機能するかどうかは、モデルの品質に左右されます。
リチウムイオンバッテリーの場合ならば、外部電圧および電流の測定によって各セルの充電量を推定しようとしていることから、セルの正確な等価回路が不可欠です(図 3)。次に示すモデルは、ピサ大学の研究者が開発した比較的単純で正確なモデルです。これにはセルの内部力学の一部が含まれていますが、アプリケーションによっては著しいことがあるヒステリシスのような挙動は除外されています。
ここまで注意深く読んできた方ならば、問題に気付いているかもしれません。このモデルは、現実の世界ではよくあるように、状態変数の連続サンプル間の直線関係が得られません。開発者はテイラー展開を利用し、拡張カルマン・フィルターと彼らが呼ぶ方法で局所的線形モデルを生成することにより、これを解決しています。
関連記事
 錠前が暗示するIoTセキュリティの3要件
錠前が暗示するIoTセキュリティの3要件
IoTの進化は創造的なプロセスと懐疑的なプロセスの2つを無視できない存在まで引き上げました。懐疑的なプロセスの筆頭は、安全性に対する懸念です。物理的な安全と個人情報の安全という両方の安全がなければ、IoTは行き詰まる可能性があります。 クラウドに生まれる新たなレイヤーの形
クラウドに生まれる新たなレイヤーの形
IoTやビッグデータコンピューティングの圧力により、クラウドには「層化」とも呼べる現象が起こっています。それはアプリケーションデータフローと実際の帯域幅、そしてレイテンシ制約という競合する課題への対応です。 ニューラル・ネットワークと力の指輪
ニューラル・ネットワークと力の指輪
指輪物語の「1つの指輪」は全ての指輪を統べる力を持ちました。ではニューラルネットワークは人工知能という力の指輪を統べる、1つの指輪なのでしょうか。 データセンターのイーサネット、パイプが太ければ十分か?
データセンターのイーサネット、パイプが太ければ十分か?
身近な存在であるイーサネットですが、データセンターでのイーサネットはその厳しい環境下で常に変化し続けることを求められています。単純に“パイプを太くする”ことでは生き延びることは難しいでしょう。 SoC設計者がIPに関心を持つべきタイミング
SoC設計者がIPに関心を持つべきタイミング
SoCが自律走行車やIoTなどの分野に進出しようとしていますが、求められる要件は分野によって大きく異なります。その結果、SoC開発者がIP(Intellectual Property)を評価・統合する方法に変化が見られます。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
- 1.5km離れた漁場をWi-Fi HaLowなどで可視化、海洋モニタリングの実証に成功
- STPAの第4ステップで忘れがちな「損失シナリオ識別」の詳細手順
コーナーリンク
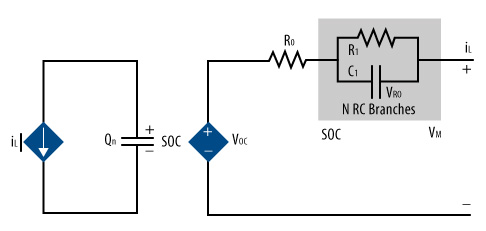 図 3. このセルの等価回路はピサ大学での研究に基づいている
図 3. このセルの等価回路はピサ大学での研究に基づいている

