無償ソフト「FreeMat」で制御工学を学ぼう:無償ソフトで技術計算しよう【制御工学基礎編】(1)(2/2 ページ)
図4は比例動作の定数kpを、図5は微分動作の定数kdを、また、図6は積分動作の定数kiをそれぞれ、0〜20に変化させた場合の変位プロフィールを描いたものです。
図4を見ると、kpが大きくなると、0から立ち上がる曲線の傾きが大きくなっていることが分かります。すなわち、比例動作は目標への収束を早めるように働きます。ただし、図4右側のkp=20を見ると、後半での収束が遅くなっているように、大きすぎる比例動作定数kpは目標値付近での収束を遅くさせます。
図5は、微分動作の定数kdの影響を示したものです。
図の左側のkd=0と中央のkd=10のケースを比べると分かるように、微分動作は変動を抑えるように働きます。ただし、図5右側のkp=20を見ると、傾きが小さくなっていること、オーバーシュートを起こしていることから、大きすぎる微分動作定数kdは収束を遅くさせることと、オーバーシュートを起こします。
図6は、積分動作の定数kiの影響を示したものです。
図の左側のki=0と中央のki=10のケースから分かるように、積分動作がないと、ki=0の例のように、目標値からずれたままとなります(オフセット)。これを補正するのが、積分動作の働きです。ただし、図6右側のki=20から分かるように、大きすぎる積分動作定数kiはオーバーシュートを起こします。
PIDコントローラーは、微分動作で変動を抑えつつ、比例動作で速やかに目標に近づけて、最終的に積分動作でオフセットをなくすように働きます。
今回の例のように、数式モデルを使い、システムの挙動を各種の設計変数で試しながら、設計する手法はMBD(Model Based Design)と呼ばれ、近年急速に普及しています。すると、コンピュータが使えなかった時代ならいざしらず、モデルさえあれば、制御工学など知らなくとも、優れた製品を設計できるのでは?という考え方もあるかと思います。
しかしながら、現実の設計は、今回の例のように簡単なものではなく、数式モデルは膨大な結果を返してきます。このとき、いきあたりばったりでは、膨大なデータを前に、迷路に迷い込むことになります。つまり、制御工学は、現実の複雑なモデルから本質を見つけ出し、解決の見通しを立てるためには不可欠なものです。そのための道具が、伝達関数やブロック線図であり、安定性や過渡応答といった評価基準です。
次回から、モデル化、伝達関数、ブロック線図について、今回使用した数式モデルを基に説明していきます。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
関連記事
 無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフトでも、かなり高度な計算ができる! 今回はインストール編。工学計算の初心者もぜひチャレンジしよう。 数式を使わないで自動制御について教えるよ
数式を使わないで自動制御について教えるよ
数式がいっぱい出てくる制御理論の習得に挫折した人は多いカモ。制御のエッセンスだけなら数式がなくても理解できる! 組み込みソフト開発の“主役”は誰に?
組み込みソフト開発の“主役”は誰に?
かつて、組み込み機器用ソフトウエアの開発は、それを専門とする技術者の手で行われていた。しかし、現在は、モデルベース設計ツールをはじめとした設計の抽象度を高めることが可能なツールを利用することで、システム設計者やドメインエキスパートであっても、組み込みソフトウエアを開発できる環境が整いつつある。本稿では、代表的なモデルベース設計ツールとその活用事例などを紹介した上で、組み込み用ソフト開発の現状についてまとめる。 無償の工学技術計算ツール「Mathcad Express」を使ってみた
無償の工学技術計算ツール「Mathcad Express」を使ってみた
設計計算や制御計算など高度な活用から、日常使いのローエンドな活用まで幅広い、無償の工学技術計算ツール「PTC Mathcad Express」を使ってみた。「単位をごっちゃにして数式を書いても計算してくれる」など便利機能がいろいろある。仕事での面倒くさい計算が楽しくなる、かも!?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
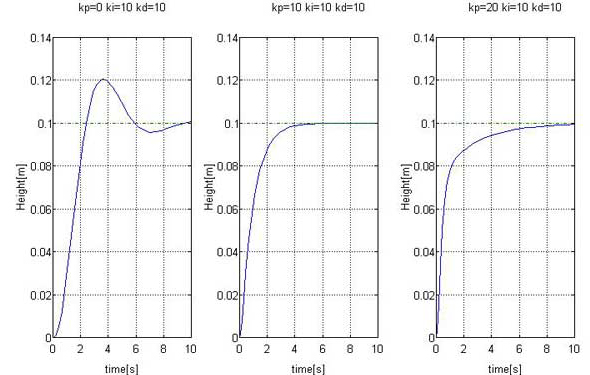 図4:比例動作kpの影響
図4:比例動作kpの影響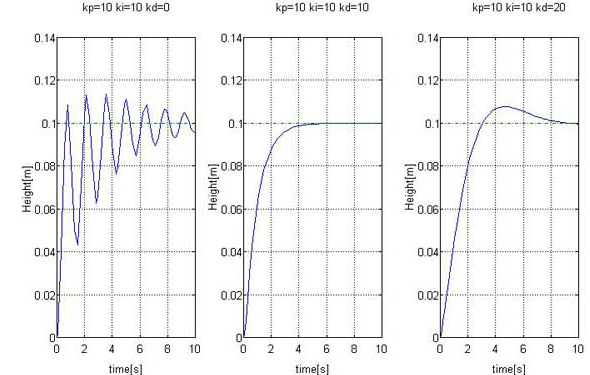 図5:微分動作kdの影響
図5:微分動作kdの影響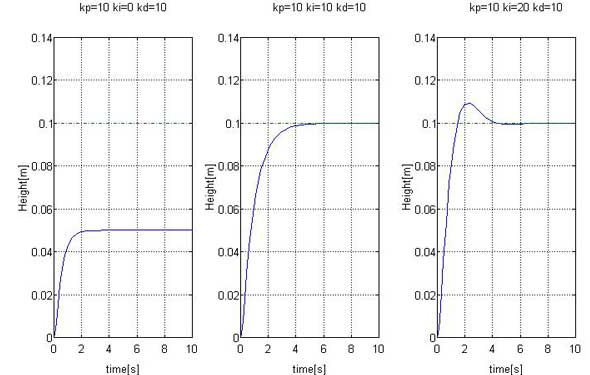 図6:積分動作kiの影響
図6:積分動作kiの影響






