モンテカルロ法で円周率を計算して、グラフにプロットする:無償ソフトで技術計算しよう【入門編】(2)(2/2 ページ)
内部定数
ヘルプに記載されている内部定数の一覧を下記に示します。これらは、所与の値として利用できます。例えば、「pi*5*5」とすると、半径5の円の面積を計算できます。また、「a=2+3*i」とすると、「a」は実数部「2」、虚数部「3」の複素数となります。上述のようにこれらは変数としても使うことが可能で、しかも警告なしで上書きされます。
- Base Constants
- E Euler Constant (Base of Natural Logarithm):自然対数の底、e=2.718281828459045
- EPS Double Precision Floating Point Relative Machine Precision Epsilon:倍精度での計算機誤差未満の数、eps 約2.2204e-16
- FALSE Logical False:false=0
- FEPS Single Precision Floating Point Relative Machine Precision Epsilon:単精度での計算機誤差未満の数、feps 約5.9604e-8
- I-J Square Root of Negative One:i,j 虚数単位
- INF Infinity Constant:inf 無限大と見なせる数、
- PI Constant Pi:円周率、pi=3.14159265358979
- TEPS Type-based Epsilon Calculation
- TRUE Logical TRUE:true=1
特に、「i」と「j」はCやJavaなどを使っている方にとって、forループ内のカウンターとして使いたくなりますが、別な変数名とするようにしましょう。これらに加えて、計算結果を示す変数ansと、数値ではないという意味の「NaN」(Not a Number)も変数として使うと上書きされるので注意が必要です。
例題:モンテカルロ法で円周率を計算する
例題として、上述の円周率にちなんで、モンテカルロ法で円周率を計算してみましょう。モンテカルロ法とは、乱数を用いてシミュレーションを行う手法で、円周率を計算するには、x座標、y座標に0〜1までの乱数を設定した多数の点を生成して、原点からの距離が1以下の範囲にある点の数を数え、これと全体の点の数との比の4倍を求めます。
FreeMatでは、下記のように2行でモンテカルロ法による円周率の計算が可能です。
--> x=rand(1000,1)+i*rand(1000,1); --> length(find(abs(x)<1))/length(x)*4 ans = 3.1400
詳しく説明すると、「rand(1000,1)」で「1000行1列の0以上1未満の乱数」を発生させます。変数xとして、「rand(1000,1)+i*rand(1000,1)」により「複素平面上に1000個の点を発生」させます(「複素平面」とは、実数部がX座標、虚数部がy座標の平面)。
次に、複素数の大きさを計算します。複素数の大きさを計算するには、共役複素数との積、つまり、虚数部の符号が反転した複素数と掛け合わせた数を計算し、その平方根を求めます。例えば、「1+i」の大きさは「sqrt((1+i)*(1-i))」としますが、「abs(1+i)」でも計算できます。
さて、大きさが1未満の点の数を選び出すには、「find(abs(x)<1)」とします(大きさが1以下ではなく1未満なのは、発生させた乱数が1未満であるためです)。こうすると、「x」という配列の中で大きさが「1」未満の要素の位置を返します。lengthは配列の行と列の内、大きい方のサイズを返します。例えば、3行2列の配列のlengthは「3」です。結局「length(find(abs(x)<1))」は大きさが1未満の点の数を示し、これを全体の点の数「length(x)」で割ると、点の数が十分多ければ、半径1の4分の1円と正方形との面積の比、すなわち「π/4」と等しいと見なせます。最後に4を掛けると円周率が求まります。
円周率を求めるだけでは芸がないので、発生した点を図に表示させてみた結果が図2です。
図2を表示させるのが下記の「ex01.m」というプログラムで、最初の3行で円周率を計算しています。つづく4〜6行で、複素平面状に大きさが1未満では青い点、1以上では赤い点となるようにプロットしています。8行目で半径1の4分の1円を描き、9、10行目でグラフの形を整えています。これらは入門編の後のグラフィックス編で説明します。
clear;N=1000;
x=rand(N,1)+i*rand(N,1);
length(find(abs(x)<1))/N*4
xin=x(find(abs(x)<1));
xout=x(find(abs(x)>=1));
plot(real(xin),imag(xin),'b.',real(xout),imag(xout),'r.');
hold('on');
plot(cos(deg2rad(0:90)),sin(deg2rad(0:90)),'k:');
axis('square');
axis([0,1,0,1]);
上の「ex01.m」ファイルは、カレントフォルダあるいはパスを設定したフォルダに保存した後、「-->ex01」と入力すると、自動で計算してグラフを表示してくれます。エディタから実行させる場合は、左から2番目のアイコンをクリック、メニューの「File→Open File」、「Ctrl+O」のいずれかでex01.mファイルを開き、エディタの左から10番目の右向き三角のアイコンをクリックするか、メニューの「Debug→Execute Current Buffer」とするか、F5キーを押すのいずれでも実行してくれます。
◇
次回は演算子、関数について説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
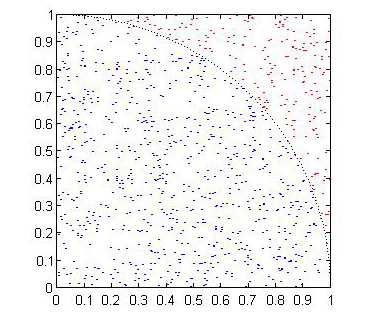 図2 モンテカルロ法による円周率計算
図2 モンテカルロ法による円周率計算






