信頼性テストを劇的に短縮するSN比の活用とは?:タグチメソッドのデータを解析しよう(3)(1/4 ページ)
データについて今まで語ってきましたが、データを活用する最も大事な意味は時間の節約ですよね。分解した変動を使ってSN比を算出すれば、時間やコストの掛かる信頼性テストを劇的に短縮できるんです。今回はその方法をお伝えします。
前回(第2回)、前々回(第1回)で、データについての考え方と、実際にデータから有効な情報を取り出す方法についてお伝えしてきましたが、いかがだったでしょうか。
さて、今回はSN比の算出により信頼性テストを劇的に短縮する方法について解説しようと思います。SN比は信頼性を表す指標そのものであり、分解した変動を使ってSN比を算出することで、信頼性テストに掛かる時間を大幅に低減することができます。
3−1.変動を分解する意味
分解の幾何学的な意味
変動の分解は非常に重要な考え方になります。SN比の説明に入る前に別の視点からもう一度説明しておきます。視覚的に理解できるように、代数幾何学的な説明をしようと思いますので、より理解しやすくなるでしょう。
前回も利用した表3-1の4個のデータで考えます。因子BをX軸にして4個のデータを座標点で示すと、図3-1になったとします。要因の水準がA1からA2に変化しても、またB1からB2になっても、特性値yの値は変化しています。
つまり因子AもBも、特性値yに対して影響力があるということが分かります。さらに、2本の破線が平行でないことから、AとBに相互作用がありそうだということも予測できます。相互作用も含め、それらの影響力を、SA、SBさらにSeなどの計算で求めるのが、変動の分解の目的です。
まず主効果のSAやSBから始めましょう。SAを図で示したのが、図3-2になります。SAとは、水準A1からA2に変化したときのデータyの変動の大きさですから、まずA1の2個のデータy1とy2の平均値mA1と、A2の2個のデータy3とy4の平均値mA2を求めます。この2つの平均値は、全平均mから等距離にありますから、全平均からの隔たりが因子Aの要因効果SAを表現していることになります。
この図で見ると、前回の数式2-7でSAを計算するときにSmを引いている理由も分かると思います。y1〜y4のデータで計算した数式2-7の第1項だけでは、破線で示すようにSmも含んでしまうからです。
SBを求めるときは、X軸を入れ替えればいいのです。因子AをX軸において全く同様に考えれば、因子Bの要因効果SBも表現できます。
Seの意味
では、Seはどのように表現できるでしょうか。図3-3を見てください。4個のデータが平行四辺形を形成していなければ、対角同士のデータの平均値は一致しません。
一致していない分がSeです。Seの中身は、AとBの交互作用や、その他未知の要因の効果ということになります。その他の要因とは、測定誤差とか測定中に環境の条件がばらついたなどの影響のことです。
SA、SB、Seの意味は、以上のようにして図で示すことができます。
変動の分解のイメージ
変動の分解の様子をイメージでつかんでもらうため、全体の変動の関係を、図3-4に表現しました。
全変動STが全ての出発点です。変動というエネルギーが存在すると考えてもいいでしょう。または4個のデータが持っている全ポテンシャルまたは全情報量といえます。それを大きな楕円で表現しました。
そこから各エネルギーSmとSAとSBを分解して切り出してしまうと、残エネルギーがSeになるということが図で理解できることでしょう。
それぞれの塊の大きさの比が、寄与率に相当します。変動を分解するというイメージを理解していただけましたか。
さて、SAとSBが独立して分離できたのは、実験の計画で要因が二元配置で直交するように仕込まれていたからです。通常は計画をきちんとしておかないと、効率的な変動の分解はできません。要因を直交させない単なる繰り返しデータでは、平均値と標準偏差しか計算できませんから、無駄になります。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 炭素繊維市場創出の“場”として機能する金沢工大 ICC、参加企業が見いだす意義
- 選択肢を絞り使い勝手を向上、貝印が設計した“刃1本”のブレンダー
- カナデビアと日鉄エンジニアリング、環境分野強化で経営統合に向けた検討を開始
- 対外2兆ドル、対内0.2兆ドル――日本の直接投資構造から見る特異性
- 必要なのは「やりたいこと」だけ 中小製造業こそDXすべき理由
- 製造業に求められる人材戦略とは 鍵を握る「スキルデータ管理」
- 永守氏がニデック完全退任、「経営者としての私の物語にピリオド」
- ニデックの会計不正の温床となった6つの原因とは? 改善計画を公表
- 会計不正問題で揺れるニデック、原因は「短期的収益を重視し過ぎる傾向」にあり
- 製造現場で作業計画自動化と無人搬送を実現するAIソリューション、日本IBMが提供
コーナーリンク

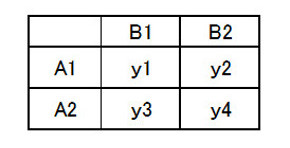 表3-1 二元配置データ
表3-1 二元配置データ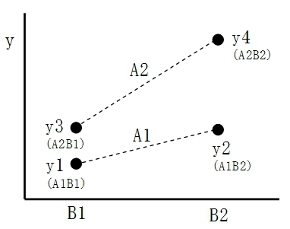 図3-1 4個のデータ
図3-1 4個のデータ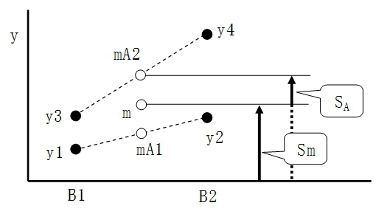 図3-2 SmとSAの幾何学的な意味
図3-2 SmとSAの幾何学的な意味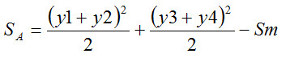 前回の数式2-7
前回の数式2-7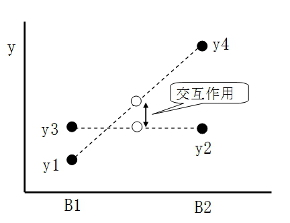 図3-3 交互作用の意味
図3-3 交互作用の意味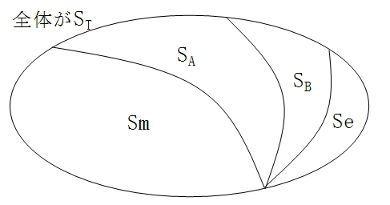 図3-4 変動の分解のイメージ
図3-4 変動の分解のイメージ



