データから正しく情報を取り出す方法を知っていますか?:タグチメソッドのデータを解析しよう(2)(4/5 ページ)
2−3.直交していれば情報を分離できる
2次元配置のデータの場合
データ数が多い場合、データの収集方法に工夫しておかないと、含まれている情報を効率よく分離できません。変動を利用してデータに含まれている多くの情報を分解して取り出すには、事前の準備が必要なのです。どういう点を注意すればよいのか、データが4個の場合で具体的に説明しましょう。
因子Aと因子Bが、それぞれ2水準(A1とA2、B1とB2のそれぞれ2個の値に設定が可能)の場合、表2-1のように4個のデータ(y1〜y4)が取得できます。そうするとデータ全体には、情報が4個入っていると見なすことができます。これをどのように分解して取り出せばよいのでしょうか。その方法を示しましょう。
データの塊を考える
データ表2-1から、因子Aの影響がどの程度なのかを推定するには、どうすればいいでしょうか。
〈因子Aの影響度〉=〈A1の平均値〉−〈A2の平均値〉
つまり図の中に破線で囲まれたデータの塊、A1の条件でのデータの塊とA2の条件でのデータの塊を考えればいいのです。計算式は以下になります。
〈因子Aの影響度〉=(y1+y2)/2 −(y3+y4)/2
同様に、因子Bの影響度も以下のように表現できます。
〈因子Bの影響度〉=〈B1の平均値〉−〈B2の平均値〉=(y1+y3)/2 −(y2+y4)/2
因子の影響度を考えるときには、表2-2で示すようなデータの塊で考えているのです。平均値を考えるときも、4つのデータ全体を1つの塊と考えていることになります。このようにデータを塊で考えますから、前回説明した変動の概念が使えること分かります。
データの塊を変動で表現する
では、いま説明したデータの塊の考え方を、変動を使って表現してみましょう。少し数式が多くなりますが、簡単な算数レベルの内容です。添え字が多いので、一見ごちゃごちゃしているように見えるだけです。基本的には、表2-2の塊ごとに変動を計算しているだけですから、添え字の意味を理解すれば、単純な計算をしていることが分かると思います。
少しだけ頑張ってください。ただ途中経過が分からなくても、最終結果だけを覚えていただければ、次に進んでも問題ありません。どうしても無理な人は、最初は以下の囲み解説の部分は飛ばしても結構です。
詳細解説
いままでの説明に従えば、全変動は平均値の変動とばらつきの変動に分解できます。データ4個でも基本は同じです。
つまり、ST=Sm+Se、自由度f は、4=1+3 になります。
このままでは、平均値と全体ばらつきの2個の情報しか得られません。自由度が3のSeには、まだ3個も情報が入っています。ですからSeを分解すれば、もっと情報を取り出すことができます。
Seには、どんな情報が入っているのでしょうか。表2-1のデータをとる場合は、A1の平均値とA2の平均値では差があるのが普通で、その差はSeに含まれる因子Aの情報となります。
では因子Aの情報を取り出すために、A1の場合とA2の場合に分けて、変動を分解する式を作ってみましょう。そのために表2-1を表2-3のように補足します。A1の平均値をmA1、A2の平均値をmA2と表します。全平均はmです。
A1とA2に関するデータは、それぞれ2個ずつですから、数式2-1を使い次のように分解できます。
この2つの式を足しあわせると、左辺はy1からy4までの2乗和ですから、全変動STになります。そして右辺は次のように表せます。
ここで右辺の前半の2項に対して再び数式2-1を適用すると
となります。
この式をよく見ると、右辺の第1項目は、平均値の変動Smですね。そして第2項目は、平均値の差の変動ですから、因子AをA1からA2に変えたときに、結果にどれだけ影響を与えるかを示しています。そこで、この第2項目を因子Aの要因効果という意味でSAと表記しますと、SAの値は次式で求められます。
ですので、つまり
従って数式2-6の後半の2項をSresAと表現すると、結局ST は以下のようになります。
ST = Sm+SA+SresA、自由度f は、4=1+1+2
これで因子Aの効果分SAを取り出すことができました。
全く同じことが因子Bについても行えますから、以下の式も成り立ちます。
ST = Sm+SB+SresB、自由度f は、4=1+1+2
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- AIエージェントが代わりに働くようになったら人は何をするの?
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
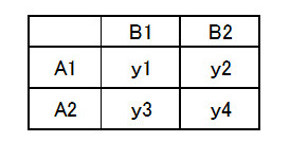 表2-1 二元配置データ
表2-1 二元配置データ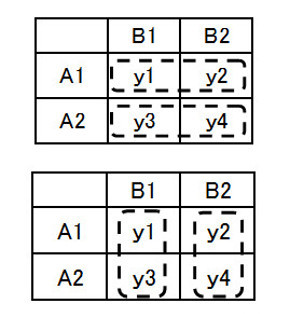 表2-2 因子Aに関するデータの塊
表2-2 因子Aに関するデータの塊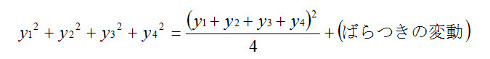
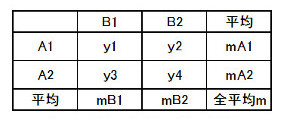 表2-3 縦の集計と横の集計
表2-3 縦の集計と横の集計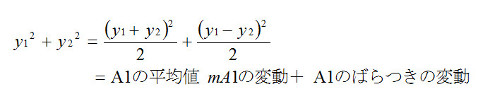 数式2-4
数式2-4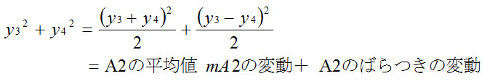 数式2-5
数式2-5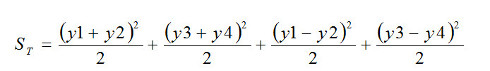 数式2-6
数式2-6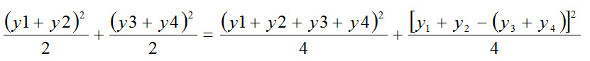
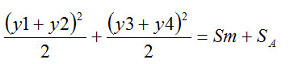
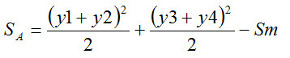 数式2-7
数式2-7



