データから正しく情報を取り出す方法を知っていますか?:タグチメソッドのデータを解析しよう(2)(2/5 ページ)
変動という塊で考える
さて、数式2-1をもっと単純に表現してみましょう。データの2乗をデータ数で割ったものを「変動」という言葉で表現してみます。
例えば、数式2-1第1項(a +b )2/2 は、「aとbの和の変動」というように表現します。
変動という言葉は少々分かりにくいですが、情報を持っている塊(ユニット)だと考えてください。ですから1個のデータの2乗であるa2 でも、分母にデータ数の1があると考えると「aの変動」と言うことができます。b2も同様に「bの変動」ですね。
従って数式2-1は、以下のように言い換えできます。
データaの変動 + データbの変動 = 平均値の変動 + ばらつきの変動
(変動 = データの2乗 / 含まれるデータの数 )
要するに、変動の形にすると分解が容易にできるのです。
記号で表現するとスッキリ
ここで変動を記号「S」 で表現してみましょう。すると、もっとすっきりした式になります。全変動「各データの変動の総和(全体の変動)」をST、「平均の変動」をSm、「ばらつきの変動」をSeとします。すると数式2-1は、以下のように簡潔になります。この式は覚えておいてください。今後もよく出てきます。
a、b という2個のデータに含まれる2個の情報は、変動という形で表現することにより、平均値とばらつきの2個の情報に分解できるということです。変動という言葉は、少々分かりにくいですが、実は非常に便利な概念です。ぜひ、理解して活用ください。
ばらつきの計算も簡単になる
変動という考え方を、今度はデータが3つ(a ,b ,c )の場合で考えます。すると変動に分解する式は、以下のようになります。
データaの変動+データbの変動+データcの変動=平均値の変動+ばらつきの変動
a2+b2+c2=ST(全変動)ですから、つまり、ST=Sm+Se です。
この式の中で最後の項の「ばらつきの変動」だけは、計算式が分かりませんね。でも安心してください。以下のようにすれば、簡単に計算できます。ばらつきの変動を、計算式が分かっている項目の組み合せで表現するのです。
数式2-2を(ばらつきの変動=全変動−平均値の変動)と変形します。
つまりSe = ST − Smです。
この式を見ると、データがどんな数字であっても、全データの変動の和(全変動)から平均値の変動を引けば、ばらつきの変動が求められることが分かります。つまり、ばらつきの変動は、直接計算しなくても簡単に求められるのです。2乗和を使う目的は、ばらつきの大きさを求めるためなのです。
この式の意味はよく覚えてください。これを応用する場面は、これからも出てきますから。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- AIエージェントが代わりに働くようになったら人は何をするの?
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
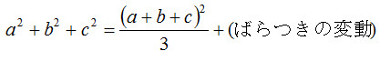
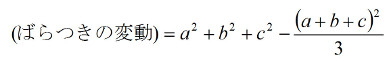 数式2-3
数式2-3



