タグチメソッドの効率化戦略が“ひと味違う”理由:本質から分かるタグチメソッド(3)(4/4 ページ)
直交表を活用したパラメータ設計
L4の直交表の説明で、直交表の意味と性質が理解できたと思います。しかし実際には、L4直交表はめったに使われません。実験できる因子数が少ないので、メリットがないからです。実験で効果を確認したいパラメータの数は、もっと多いのが普通でしょう。だからといって、むやみに大きな直交表を使うのは得策ではありません。実験の数と実験できる因子数のバランスから考えると、使いやすいのはL18直交表だといわれています。
ここでL18直交表を使ったパラメータ設計の流れを簡単に説明しておきます。細かい手順の説明は、本冊子の目的ではないので省きますが、全体の流れだけを理解してください。
表6に示すように、使用できる因子の数はA〜Hの8個ですから、実験してみたいアイデアなどを8項目用意します。組み合わせが指定された実験数は18ですから、18回の実験を行い18種類のデータを取ります。1回の実験にはノイズ因子を変えた複数のデータ(表6では8個)が含まれています。その複数のデータを使ったデータ処理で、平均値とSN比にまとめます。
次に、18個の平均値とSN比のデータを使い、L4直交表で説明したように組み合わせを変えて計算します。すると8項目の因子の効果の有無が定量的に分離できます。それを図4に示す要因効果図に表現します。図は、横軸が実験した要因の水準で、縦軸がSN比です。
ロバスト性の高い設計とは、どのような条件なのか。それは、この要因効果図から簡単に読み取れます。SN比の高い条件を組み合わせればいいのです。同様な要因効果図を平均値に対しても作成すれば、2つの要因効果図から最適条件の決定が可能になります。
以上がパラメータ設計全体の流れです。詳しい説明は専門書を参照してください。直交表の性質を活用して再現性のチェックができる手順も用意されており、実験結果の信頼性も確認できるので安心です。
直交表の別の利用法
直交表の別の利用法も、説明しておきましょう。そのために直交の性質を、別の視点から見てみます。表7のL9直交表で説明しましょう。実験回数は9個で、使える因子の数は4個までです。しかし各因子の条件は3種類まで変化させられます(3水準)。
このL9直交表が「直交している」ことを模式的に示したのが図5です。L9直交表が使える因子は4個なので、本来は4次元になるのですが表示できません。そこで、3個の因子を立方体の3個の稜(りょう)線に対応させて表現した図です。9個の球体は、実験ナンバー1〜3で指定された9個の座標位置に置かれています。
図5を見ると、9個の球体をどの平面に投影しても重ならないように配置されています。これが直交という性質の立体表現です。つまり直交させるとは、空間の中に均一な距離を持った座標点を設定することなのです。L9の場合は因子が4個ですから、4次元空間での均一配置ということになります。もっと大きな直交表を使えば、n次元空間での均一配置も可能になるのです。
n次元空間での均一配置が可能という性質を、うまく使って成功している方法があります。1つはシミュレーション実験です。現物を使った実験はせいぜいL18ぐらいが限度ですが、シミュレーションならもっと多くの因子を同時に検討することが可能です。L128やもっと大きい直交表も活用できます。
直交表は、n次元空間の均一配置点の座標を決定する
⇒さまざまな効率化ツールに活用できる
⇒一例)ソフトウェアのバグチェック
また、ソフトウェアのバグ確認にもこの性質を活用できます。パラメータが多過ぎてすべての組み合わせでデバッグできない場合、可能な作業量でバグ発見効果を最大に上げるために直交表を使う企業が増えてきました。n次元空間での均一配置が可能という性質は、固有技術に頼らないデバッグ作業に最適だからです。
◇ ◇ ◇
前回と今回で、タグチメソッドの発想法とそれを実現する手法についてみてきました。目的のない手法に意味はありません。未然防止と効率化というタグチメソッドの目指すものを忘れないようにしましょう(次回へ)。
⇒前回(第2回)はこちら
⇒次回(第4回)はこちら
⇒本連載の目次はこちら
筆者紹介
長谷部 光雄(はせべ みつお)
品質工学会会員、日本信頼性学会会員
株式会社リコーで技術開発センター所長を歴任後、技師長および顧問として同社のグループ会社全体を対象に品質工学の指導と推進を担当。
主な著書に『ベーシックタグチメソッド』(日本能率協会マネジメントセンター、2005年)、『技術にも品質がある』(日本規格協会、2006年)、『品質力の磨き方』(PHP研究所、2008年)など多数。
関連記事
 時間もお金もなくても実践できる信頼性テストの方法とは?
時間もお金もなくても実践できる信頼性テストの方法とは?
時間もない。お金もない。頑張って信頼性テストをやってみれば、市場に出てから製品にエラーが。ああ、苦労してこんなことやって、本当に意味あるの? 実は、“使える”方法が、ちゃんとあります。 「タグチメソッド」生みの親、田口玄一博士の1周忌追悼シンポジウム開催
「タグチメソッド」生みの親、田口玄一博士の1周忌追悼シンポジウム開催
「タグチメソッド」の生みの親である田口玄一氏の功績をたたえる追悼シンポジウムが開催され、品質工学の祖であるとともに優れた統計学者でもあった同氏の功績を振り返った。 タグチメソッドで品質向上の最適条件を見つける
タグチメソッドで品質向上の最適条件を見つける
モノづくり現場で発生している品質不良を改善し、不良率半減を目指そう。品質改善のツールはあくまでもツールであって、それに振り回されてはいけない。本連載は品質改善コンサルタントによる品質改善の王道を解説する。 品質改善プロジェクトに失敗は許されない
品質改善プロジェクトに失敗は許されない
モノづくり現場で発生している品質不良を改善し、不良率半減を目指そう。品質改善のツールはあくまでもツールであって、それに振り回されてはいけない。本連載は品質改善コンサルタントによる品質改善の王道を解説する。 成功する品質改善プロジェクト体制はここが違う
成功する品質改善プロジェクト体制はここが違う
モノづくり現場で発生している品質不良を改善し、不良率半減を目指そう。品質改善のツールはあくまでもツールであって、それに振り回されてはいけない。本連載は品質改善コンサルタントによる品質改善の王道を解説する。 製造ITは品質改善に役立つのか
製造ITは品質改善に役立つのか
グローバル展開が必然のものとなった日本のモノづくり企業。海外拠点との生産性の違いが課題として立ちはだかる。品質改善や不良品対応を「匠の技」として祭り上げていないだろうか。これではグローバル展開は難しい。ITによる適切な道具立てとそれを支えるマインドセット、さらにマネジメントの変革が解決には必要だと専門家は説く。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- AIエージェントが代わりに働くようになったら人は何をするの?
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク

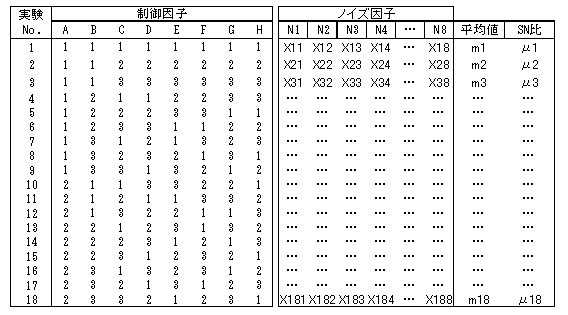 表6 L18直交表の例
表6 L18直交表の例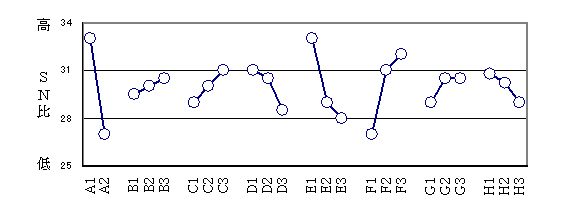 図4 実験した8個の因子の効果を表現する要因効果図
図4 実験した8個の因子の効果を表現する要因効果図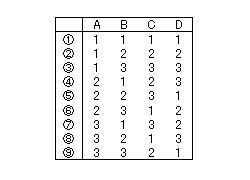 表7 L9直交表
表7 L9直交表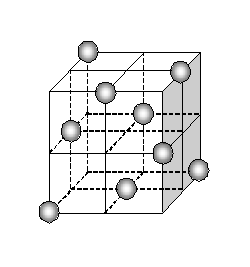 図5 L9直交表の模式図
図5 L9直交表の模式図




