タグチメソッドの効率化戦略が“ひと味違う”理由:本質から分かるタグチメソッド(3)(3/4 ページ)
ロバスト性評価の場合
ではロバスト性評価法に応用し、データ数を減らす考え方を説明しましょう。以前から行われている信頼性テストや寿命テストは、テスト期間中にどのような問題がどのくらい発生したかを計測します。時間軸に対する問題の発生数のデータです。
そしてワイブル確率紙などの統計的な処理を行い、図3上のようなイメージを描きます。つまり、横軸が使用時間で縦軸が問題発生数からなる分布図です。
注:ワイブル確率紙とは、ワイブル分布やそのグラフなどで統計的な処理を行う際に用いるグラフ。
しかし、このデータを作成するのは大変な作業です。多くの時間を使い多数のデータを収集しなければなりません。毎日生産を続けている製造工程や、市場のデータが自動的に収集できるシステムが完備されているなら可能です。しかし新製品の開発期間のように、長期間にわたる大量のテストをできない場合の方が、現実には多いのです。従って図3の上半分は、分かりやすい表現ですが実用的ではないということになるのです。
このような実用性の低いデータではなく、時間軸からノイズ因子の軸に変換するとどうなるでしょうか。図3下半分は、どのような使い方をするとどの影響があるかを示すやり方です。つまり問題を起こす原因成分に分解する考え方です。
このデータは、ノイズ因子ごとに両極端条件のデータを取ったものです(表4)。温度変化には何%の影響を受けるか、表面が汚れるとどのくらい機能が低下するかなどを個別に測定するのです。温度を意識的に変化させた測定、わざと汚した測定ですから時間はかかりません。その影響度を対象物と相対比較すればいいので、非常に短期間で終了します。
ロバスト性評価の座標軸変換とは
問題発生件数のデータではなく、原因成分の寄与率軸に転換すること
直交表とは
2番目の工夫に入りましょう。2番目の工夫とは、多くのアイデアを効率的に評価する実験についてです。直交表をご存じの方も多いでしょうが、念のため直交表の仕組みを簡単に説明しておきます。
表5に一番簡単なL4直交表を示します。表の縦列の数字1〜4は、実験ナンバーを示しています。つまりL4直交表とは、4回の実験条件を指定するための表であることが分かります。表の行にある因子A〜Cは、実験条件を指定する因子名です。3種類の因子に関する実験であることが分かります。そしてA1とかB2とあるのは、因子の条件を2つの値(例えばA1とA2、これを水準といいます)に変化させて実験することを示しています。このように当てはめることを「直交表に割り付ける」といいます。最終の欄のX1〜X4は、実験ナンバーごとに指定された条件のデータです。
直交表の実験では、このように実験条件が規則的に指定されますから、例えば実験2では、必ずA1、B2、C2の条件で実験しなければなりません。規則に従ったデータを取るからこそ、実験後の解析によって有効な情報を引っ張り出すことができるのです。
この直交表は、どのような性質を持っているのでしょうか。実験ナンバー1と2の条件を足してみましょう。すると、2×A1、B1+B2、C1+C2となります。つまり因子Aに関してはA1だけを使いますが、BとCに関しては1と2の値を両方使います。ですから、実験ナンバー1と2のデータの和には、因子A1の情報しか含まれていないと考えられるのです。
同様に考えれば、実験3と4のデータの和には因子A2の情報だけが、実験1と3のデータの和には因子B1の情報、実験1と4のデータの和には因子C1の情報しか含まれていないと考えられます。このようなお互いに対して独立している性質を「直交している」といいます。
直交とは、因子同士が独立して変化できること
実験1+実験2=2×A1+(B1+B2)+(C1+C2)
因子BとCの効果は、1と2で打ち消されている
結局、因子A1の効果だけが抽出できる
データX1〜X4が直交しているという性質を使って、4個のデータの組み合わせ方を変えて計算することで、3つの因子ABCの効果を引き出すことができます。これが直交表を使った実験のメリットです。極端ないい方をすると、4個のデータから3個の因子の効果が計算できるのです。実験に直交表を活用すると、非常に効率がいいことが分かります。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- AIエージェントが代わりに働くようになったら人は何をするの?
- 永守氏がニデック完全退任、「経営者としての私の物語にピリオド」
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
コーナーリンク

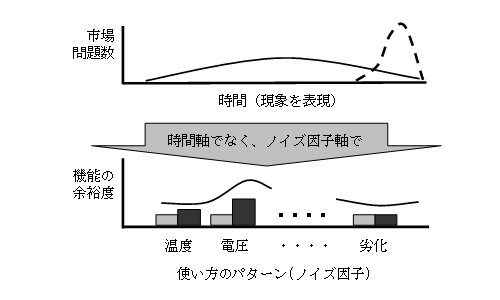 図3 ロバスト性評価でも、座標変換で情報が増える
図3 ロバスト性評価でも、座標変換で情報が増える 表4 ノイズ因子ごとの影響度データ
表4 ノイズ因子ごとの影響度データ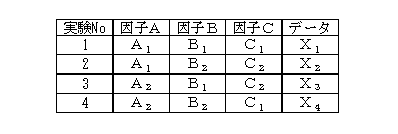 表5 L4直交表の例
表5 L4直交表の例



