ブンさんの家宝じゃないよ、分散の加法性!:公差解析 基本中の基本(3)(2/4 ページ)
ブンさんの家宝とは
アズーたちが工作室に戻ってくると、紺色のベスト&スカート姿の社員らしき若い女性……?
あのぉー『ブンさんの家宝ってなあに?』って、いま放送があったんですけどぉー……ていうか、あたしぃ、もしかして、それ知ってんじゃね? トカ思ってぇ
……明らかに、あのおじさんが無理やり変装した、ちょっと痛々しい姿でした。
ちょっとおじさん! 他人のフリしてないで、とっととこっちに来て続きを教えなさいよ!
ココがおじさんの頭を強引につかむと、カツラがすっぽ抜けました。
イテテテ……! ミーはおじさんじゃなくて、小悪魔さん! この会社に住む小悪魔さんなのYO!
あー、おじさん! 放送聞いて、また来てくれたんだ。よかったぁ!!
おじさん、昨日途中までいいかけてたやつの続きを教えなさいよ。何で二乗和平方根はあの計算が成り立つワケ?
だからぁーっ!! ミーは、小・悪・魔・さ・ん!
いま、放送聞いた人が、『それは“分散の加法性”のことかな?』っていってたよ! 最初はびっくりしたけど、放送してみるもんだね
ピンポン、正解! じゃあ今日こそ説明シヨウ! まず『分散』ってシッテル?
知らなーい
ユーは、あっさり答え過ぎ! 分散はね、サンプリングしたデータ(寸法測定データ)から計算するんだよ。デイちゃん、何かサンプリングデータはあるカナ?
部品Aのならありますよ〜。見てくださいな
このデータの平均値は? 4.848621ダネ。30個それぞれのデータと、コノ平均値って、どれくらい離れているのカナ?
それぞれのサンプル値から平均値を引けば分かるじゃないの
イエース! そうなの! それを『偏差』っていうんだYO。平均値から偏って生まれた差ダカラネ。この平均値からの離れ具合が全体的に多いか少ないかで、バラツキが多いか少ないかがワカルのよね〜
[サンプル値]−[平均値]=[偏差]
『全体』っていうけど、全部足したらマイナスとかプラスとか交ざらないか? それは、技術者ではないオレでも分かる
ボーイ、正解だYO! この偏差は二乗してから足すの。それが『偏差平方和』ネ。で、この和をサンプルの数で割って平均値を出してちょうだい! これが『分散』ネ!
[偏差]2の総和=[偏差平方和]
今回は約0.044になりますネ〜
[偏差平方和]/[サンプル数]=[分散]
じゃあ、0.044をサンプル数の30で割ると、大体0.00147になるね!
ちなみに分散は二乗した数を足してるデショ? 平均値からの離れ具合を評価するなら、元に戻した方がイイよね
平方根(√、ルート)だね!
イエース。平均値を平方根で取った値が『標準偏差(σ)』っていうのYO〜。ということで、デイちゃんのサンプルは、標準偏差が約0.038になるのよ。イエス!
小悪魔さんはね、あの5Sの張り紙の裏からコッソリ見てたのYO。午前中に集計したデータに、全体の0.3%のところに線を引いてたデショ? アレって『3σの領域』ってあの天使さんは、いってたのね
……あくまで、午前中のおじさんとは別人なのね
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
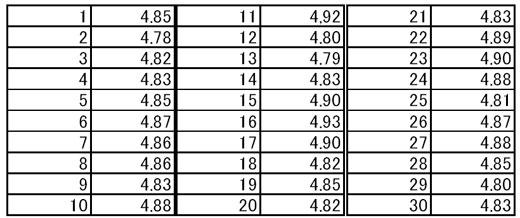 表1 部品Aのサンプリングデータ
表1 部品Aのサンプリングデータ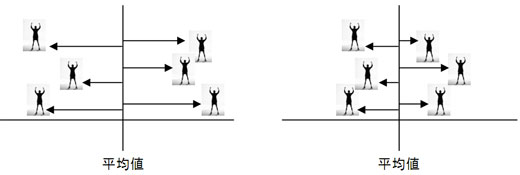 図2 「平均値からの離れが多い=標準偏差大」 「平均値からの離れが少ない=標準偏差小」
図2 「平均値からの離れが多い=標準偏差大」 「平均値からの離れが少ない=標準偏差小」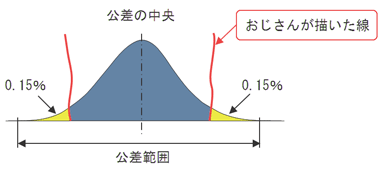 図3 午前の部 復習
図3 午前の部 復習





