3人中2人が間違える!? 片持ちばりの計算をしよう:設計者CAEを始める前にシッカリ学ぶ有限要素法(7)(1/3 ページ)
今回は、これまでの解説内容を実践してみる。3人中2人が間違えるという片持ちばりの変形量計算にチャレンジ。
前回は「メッシュサイズが解析の精度を大きく左右する」ということを説明しました。最近の設計者向けのCAEソフトウェアはメッシュサイズが適当に決定されて、メッシュの「顔」も見えないものが多くあります。だからこそ、メッシュサイズを意識して解析に臨む必要があるのです。
さらに大切なことは、「解析を1回コッキリで終わらせてはならない」ということです。実験だって何度か同じことをやって、平均値を取りますよね。解析だって同じことです。メッシュサイズを変えて何度か解析しなければならないのです。
この連載も今回が7回目。ずっと解説ばかりだったので、今回は実際に有限要素法のソフトウェアを使って、これまで解説したことを実践してみたいと思います。皆さんがお使いのソフトウェアでもぜひ同じような実験をしていただければと思います。
片持ちばりの変形量を手計算してみる
まずは解析するモデルから決めていきましょう。連載記事「仕事にちゃんと役立つ材料力学」で何度か登場した「片持ちばり」とします。寸法は図1のとおり。
この連載で「イメージすることが大切」であると何度も強調してきました。ここでもぜひイメージしてみてください。これくらいの鉄のカタマリだと、ズッシリと重いです。そしてヒンヤリと冷たい……。それが頑丈な壁にシッカリと張り付いています。この張り付き方が半端ではなく、もう何をしても外れないようにシッカリとくっついているのです。こんなイメージは解析には直接役に立たないことですが、エンジニアリング力を鍛えるための“はじめの一歩”だと思っています。
ここで「軟鋼」について少しだけ説明しておきます。軟鋼とはいわゆる普通の「鉄」のことです。普通の鉄とは多分、アナタの想像している鉄そのものです。橋や建物に使われているものです。「軟鋼」って「軟」という字があるので、何だか柔らかそうなイメージがありますよね。学問的にいうと「鉄」は「純鉄(不純物のない鉄)」をいいます。純鉄は軟らか過ぎて工業用の材料として強度部材に使うことができないのです。鉄に炭素などをほんの少し混ぜることによって強さをアップさせることができます。そうなると「鉄」は「鋼(はがね)」と呼ばれるようになります。炭素の含有量が0.13〜0.2%だと引張り強度が38〜44kgf/mm2くらいになります。
片持ちばりのような構造には理論解があり、手計算で荷重が掛かったときの挙動を求めることができます。一般的な材料力学の教科書には必ずこの公式が書かれています(図2)。
何か数式がややこしい感じがします。イチ(1)やエル(l)やアイ(I)が入り交じっているので注意が必要です。この公式を日本語で書き直してみましょう。何となく親しみやすくなります。
片持ちばりの先端に100N(ニュートン)の力が掛かるとします。100Nは約10kgf。ぜひその重さもイメージしてみてください。スーパーマーケットでお米を買ったことがあるでしょう? 大体5kg入りの米袋2つ分で、約10kg。結構な重さですね。
さて、これまで出てきたことのない言葉が出てきました。「断面2次モーメント」です。断面2次モーメントとは、上の公式でも示したように「I(アイ)」で表され、慣性モーメントともいいます。極めてカンタンにいうと、「はりの曲げやすさや曲げにくさを表す数字」ということになります。この数字はもちろん、はりの断面形状によって変わります。はりの断面の寸法を固有の公式に代入すると、断面2次モーメントが得られます。主な断面形状とその断面2次モーメントの公式は機械設計便覧やインターネットでカンタンに調べることができます。
公式集−断面性能(面積・断面係数・断面2次モーメント・断面2次半径)
今回のはりの断面は長方形。よって以下の公式より断面2次モーメントを求めることができます。
「断面の幅」と「断面の高さ」は、はりをどういう方向で配置するかによって変わってきます。もちろん斜めに置くという場合もありますが、ここでは説明しやすくするため、断面を90度回転させる場合で考えてみましょう。横置きと縦置きの場合で、それぞれの断面2次モーメントを計算します。
横置きよりも縦置きの方が大きな断面2次モーメントとなっています。縦置きの方が曲がりにくいことは経験的に分かりますよね。公式集にない断面については、僕がまだ若手だったころは断面を長方形に分割して表を作って手計算で求めたものです。最近ではいろいろとツールもありますので任意形状の断面2次モーメントが必要な場合は、皆さんで調べてみてください。
断面2次モーメントの公式の由来については、以前にもこの連載で紹介させていただいたことのあるJIKOさんのホームページ(CAE技術者のための情報サイト)がとってもいいです。長方形断面の断面2次モーメントが例題として掲載されています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- NVIDIAとダッソーがCEO対談 産業AI基盤構築で戦略的パートナーシップ締結
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 設計者を支える3つのAI仮想コンパニオン 探索×科学×実現で製品開発を伴走
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 強度設計の出発点 “計算”より先に考えるべきこととは?
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 幾何公差の基準「データム」を理解しよう
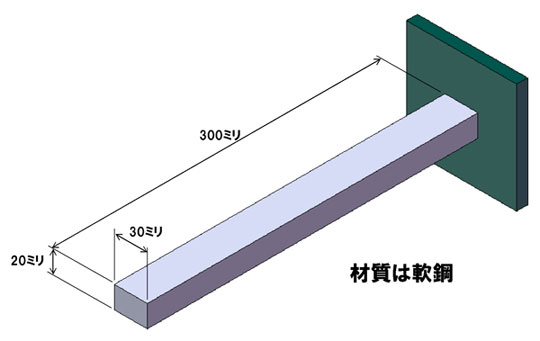 図1 片持ちばりとその寸法
図1 片持ちばりとその寸法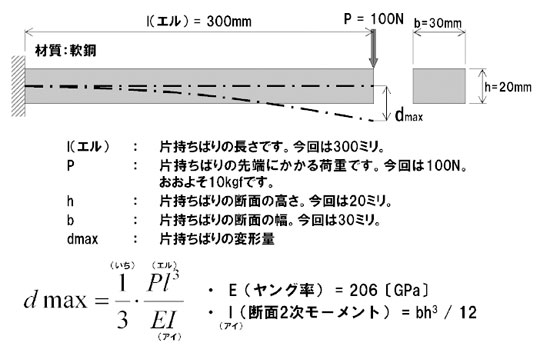 図2 片持ちばりの変形量を計算するための公式
図2 片持ちばりの変形量を計算するための公式 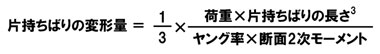

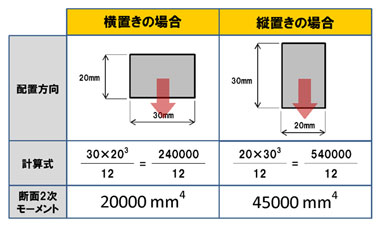 図3 横置きと縦置き、断面2次モーメント比較
図3 横置きと縦置き、断面2次モーメント比較 





