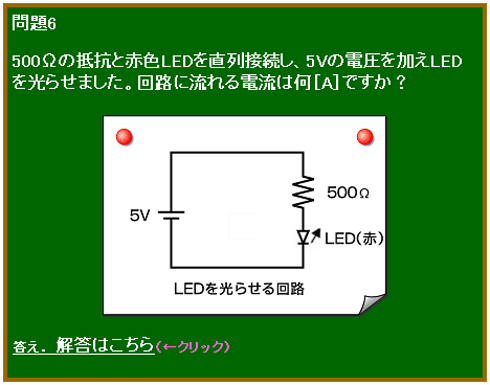
【問題6】 LEDを光らせる回路:完全マスター! 電子回路ドリル(6)
抵抗を直列接続したときの各部の電圧は抵抗に比例して分圧される。これを応用すると抵抗の変化を電圧の変化に変えることができる
【問題5】の解答
前回の宿題【問題5】は、3つの抵抗を直列接続して電圧を加えた際、各抵抗の両端の電圧値を求める問題でした。皆さん解けましたか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、電気・電子回路の基礎知識を身に付けてください。
それでは、解答を発表します!
【問題5】の解説
【問題5】は、抵抗の直列接続と分圧についての問題です。それでは解説に入ります。
【問題4】を解いたように、最初に回路に流れる電流I[A]を求め、それから“オームの法則”により各抵抗の両端の電圧を求めましょう(図1)。
回路の合成抵抗をR[Ω]としたとき、電流I[A]は次のように求められます。
R1[Ω]の両端に現れる電圧V1[V]は、
となり、式の上では電流I[A]が消去されます。ここで、抵抗を直列接続したときの各部の電圧は、抵抗に比例して分圧されることが分かります。
同様に、V2[V]とV3[V]は次のように求められます。
各抵抗の両端に加わる電圧は抵抗に比例するので、抵抗が大きいほど電圧は大きくなります。
それでは、ここまでの解説を基に【問題5】を解いてみましょう。
各抵抗に加わる電圧は、次のように“抵抗の比”によって求められます。
これにより、V1[V]は「1.67V」、V2[V]は「3.33V」、V3[V]は「5V」となります。
抵抗の直列接続による分圧を応用すると、抵抗の変化を電圧の変化に変えることができます。例として、光導電素子であるCdSセル(画像1)を図2のように接続すると、光量が電圧に変換されます。いわゆる“センサ回路”です。
CdSセルは光が多く当たるほど抵抗が小さくなる素子なので、図2(a)の回路では光の量が多いほど低い電圧が、図2(b)の回路では光が多いほど高い電圧が出力されます。
次回までの宿題 ― 【問題6】
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- チップレットでASIL Dを支援する車載SoC技術を開発
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
- 1.5km離れた漁場をWi-Fi HaLowなどで可視化、海洋モニタリングの実証に成功
- STPAの第4ステップで忘れがちな「損失シナリオ識別」の詳細手順
コーナーリンク

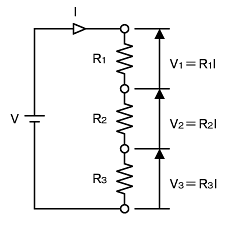 図1 抵抗の直列接続と電圧
図1 抵抗の直列接続と電圧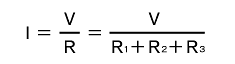
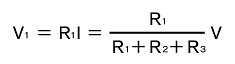
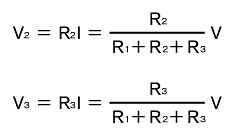
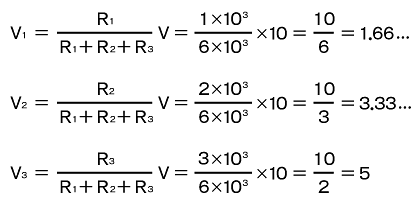

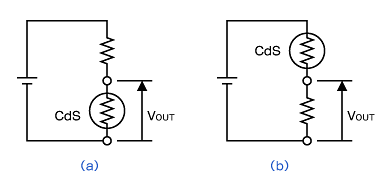 図2 光センサ(CdS)の基本回路
図2 光センサ(CdS)の基本回路