確率統計で考える公差設計：若手エンジニアのための機械設計入門（7）（2/2 ページ）

[土橋美博／スワニー，MONOist]

標準正規分布とは？

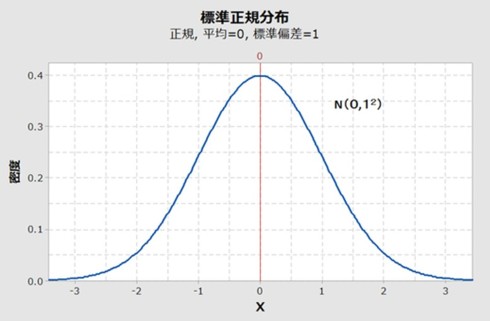
　正規分布とは、データが平均値を中心に左右対称にバラつく、滑らかな山形のグラフです。このうち、特にシンプルな形のものが「標準正規分布」と呼ばれます。平均値（μ）＝0、標準偏差（σ）＝1のとき、この分布を「N（0，1²）」と表記します。

図3　標準正規分布［クリックで拡大］

　図3は、標準正規分布のグラフを示しています。このグラフの横軸は、標準偏差の何倍に相当するかを表しています。そのため、±1の区間では1倍、±2の区間では2倍、±3の区間では3倍となります。

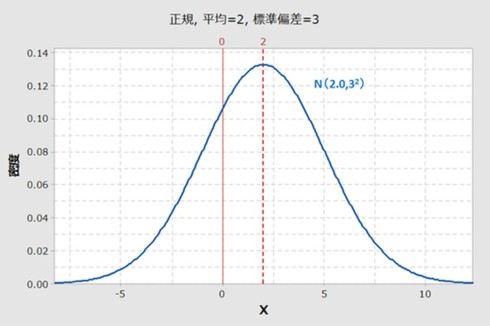
　標準正規分布は、「平均が0、標準偏差が1」に統一された、特別な正規分布の形です。しかし、実際に発生する正規分布をヒストグラムで表すと、平均値は0ではない場合が多く、図4のようになります。

図4　実際の正規分布［クリックで拡大］

　不良率を求めるには、「標準正規分布表」を使用します。標準正規分布表は、「標準正規分布において、ある値以上となる確率」を示しているため、図4のような任意の平均値と標準偏差を持つ正規分布から、そのままでは不良率を求めることができません。

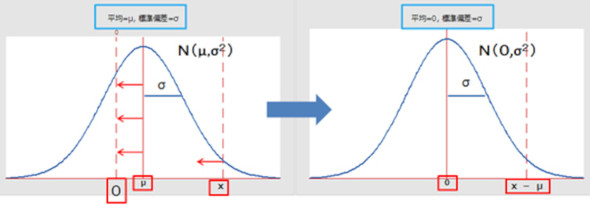
　そのため、実際の正規分布（平均値μ、標準偏差σ）を標準正規分布に変換する「標準化」を行う必要があります。標準化によって、任意の正規分布を「平均0、標準偏差1」の形に変換できるようになり、標準正規分布表を用いて不良率を求めることが可能になります（図5）。

図5　標準正規分布表［クリックで拡大］

　標準正規分布表を使用するためには、正規分布を標準正規分布へ変換する、標準化を行う必要があります。そのイメージを図6に示します。

図6　標準正規分布への変換（標準化）［クリックで拡大］

不良率を求める

　数学のテストがありました。生徒全体の平均点は70点、点数のバラつき（標準偏差）は10点で、点数は正規分布に従っているとします。

　先生はこう言いました。「60点未満は補習です」。テストの点数は、実施するごとに平均点やバラつきが異なるため、単に「60点」という数値だけでは、その良しあしを判断できません。そこで使うのが「標準化」です。つまり、その点数が平均からどれだけ離れているかを示す必要があります。

Z＝（60−70）／10＝−1.0

　60点は、平均より1つ分（1σ）下の位置にあることを意味します。Z＝−1.0以下に該当する人が全体の中でどれくらいいるかは、標準正規分布表で確認します。Z＝−1.0のとき、左側の確率は15.9％です。つまり、このテストでは約15.9％の生徒が60点未満で不合格になると予測できます。

　この考え方を製造業に置き換えると、次のような対応関係になります（表1）。

	テストの話	製造の話
	点数のバラつき	寸法のバラつき
	不合格ライン60点	上限／下限の公差
	不合格者の割合を予測	不良率を予測
表1　標準正規分布表から不良率を求める

---

　次回は、実際のモデルから不良率を推測します。（次回へ続く）

⇒ 連載バックナンバーはこちら

著者プロフィール

土橋美博（どばし よしひろ）

半導体組み立て関連装置メーカー、液晶パネル製造関連装置メーカーを経て、「メイドINジャパンを、再定義する。」有限会社スワニーに入社。CIOとして最新デジタルツールによるデジタルプロセスエンジニアリング推進に参画する。

ソリッドワークス・ジャパンユーザーグループ（SWJUG）、ワールドワイドのソリッドワークス・ユーザーグループネットワーク（SWUGN）のリーダーも務める。