ボールねじを使った1軸リニアアクチュエーターの性能向上:CAEと計測技術を使った振動・騒音対策(15)(5/6 ページ)
1軸リニアアクチュエーターのシミュレーション
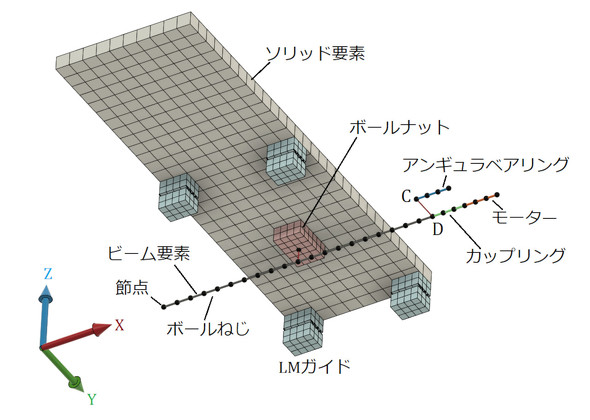
1軸リニアアクチュエーターは、ボールねじを含めて動的なシミュレーションが可能です。有限要素法モデルを図19に示します。ボールねじ、モーター、カップリング、アンギュラベアリングはビーム要素でモデリングします。AnsysのBEAM4を使いました。ステージとLMガイドはソリッド要素を使いました。ビーム要素を使っていることから、節点の運動の自由度は6個あり、X軸変位、Y軸変位、Z軸変位、X軸周りの回転、Y軸周りの回転、Z軸周りの回転となります。
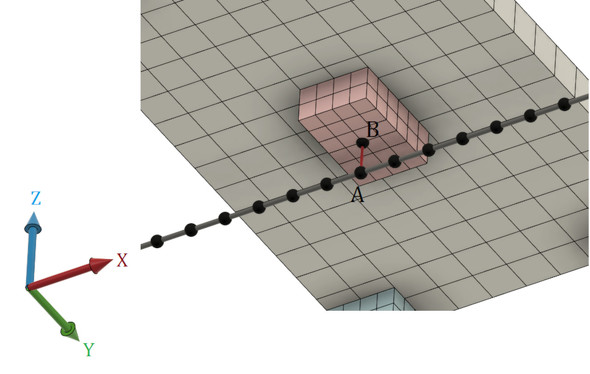
図20にボールねじのモデリングを示します。
節点Aの回転角と節点Bの変位を特殊な式で関連付けます。「拘束方程式」と呼ばれており、次式となります。説明のため離していますが節点Aと節点Bは同一座標です。
式5の意味するところは、節点Aが1回転すると節点B、つまりボールナットがねじのリード分進むということになります。これでねじ対偶を有限要素法モデルに組み込むことができました。
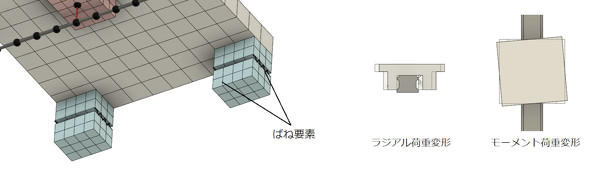
図21にLMガイドのモデルを示します。LMガイドは2つのブロックとそれらを結合する2本のばね要素から構成されています。LMガイドは内部のボールがつぶれることによって、ラジアル荷重による変形とモーメント荷重による回転変形が発生します。これらの荷重に対する変形量と回転角はLMガイドのメーカーに問い合わせれば剛性値として教えてくれます。この剛性値となるように、ばね要素のばね定数を決定します(参考文献[3])。
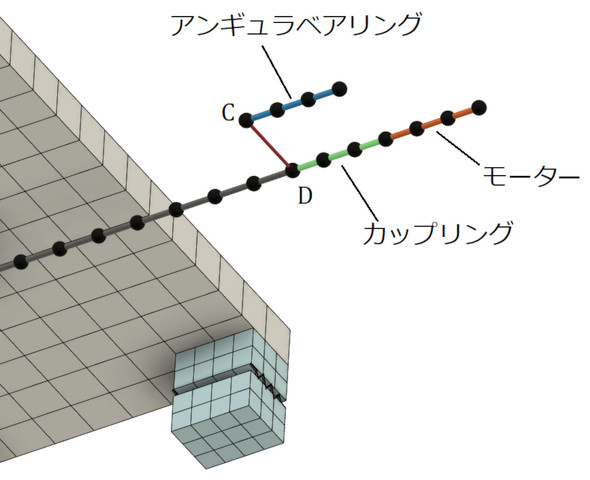
図22にモーター近傍のモデリングを示します。ビーム要素は、2つの断面二次モーメント(X軸周りの断面二次モーメントとY軸周りの断面二次モーメントですね)と断面積を各要素に個別に設定できます。2つの断面二次モーメントの和は回転に対する断面二次モーメント(断面二次極モーメント)になり、回転剛性を表現できます。モーター内のローター(回転子)の慣性モーメントはモーターのカタログに載っているので、モーターのビーム要素の断面二次モーメントと密度を調整することでローターの慣性モーメントをモデル内に忠実に表現できます。カップリングもねじり剛性がカタログに載っているので断面二次モーメントを調整することで表現可能です。図22では、アンギュラベアリングとカップリングを離して描いていますが、両者は同一軸上に配置され、節点Cと節点Dは同一節点となります。アンギュラベアリングはスラスト荷重に対する変形を表現したいので、断面積とヤング率で調整します。
以上でボールねじを使った1軸アクチュエーターの有限要素法モデルができました。モーターの節点をX軸周りに少しだけ回転すると(微小変形問題ですね)ステージはX軸方向に進みます。モーダル解析をすると1次のモードとして図14のような変形形状が現れます。1次のモードの振動数は、実際の機械においてサーボパックのゲインをどんどん大きくしていって、サーボ系を発振させたときの振動数と一致します。ただし、シミュレーション値と実験値を一致させるには、LMガイドなどの各要素のばね定数の値は、メーカーが教えてくれるものを使うのではなく、自分でばね定数に相当する値を測定して使う必要があるようです。
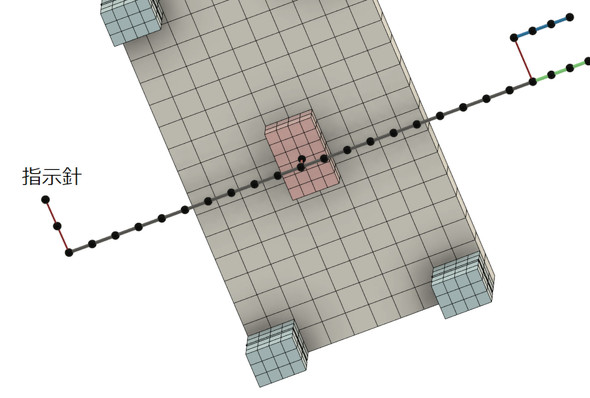
ビーム要素はねじり変形をするので、図23のように指示針(密度はゼロ)を付けておくと、ボールねじの回転角が分かります。モーダル解析による変形形状を見ることで、どこが大きく変形しているかが分かります。以前、「モーダル解析は振動対策のヒントにならない」とお話しましたが、この場合、1次のモードがサーボパックのゲインを上げてサーボ系を発振させたときの状態と一致するため、ゲインを上げたいときにどこを変更すればよいかが分かります。
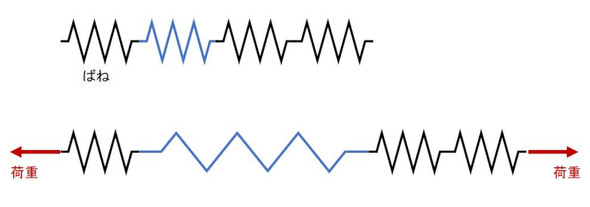
ボールねじ、LMガイド、アンギュラベアリング、カップリングなどの変形要素は、よく見るとばねの直列つなぎになっています。図24のような形です。以前お話ししたように、これらのばねのうち1つでもばね定数が小さいと全体のばね定数が小さくなってしまいます。どんなにゴツゴツとした1軸テーブルを設計したとしても、1つでも剛性の低いパーツを使うと台無しになってしまいます。構成する変形要素の剛性の凸凹をなくした設計が、最適に近いものになると考えます。
参考文献:
- [3]高橋|メカトロ機器で使用される機構要素部品の有限要素法モデル(LMガイドのモデル化)|日本機械学会 2006年度年次大会(2006-9)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

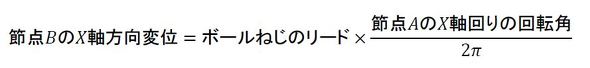 式5
式5