ボールねじを使った1軸リニアアクチュエーターの性能向上:CAEと計測技術を使った振動・騒音対策(15)(3/6 ページ)
1軸アクチュエーターの剛性
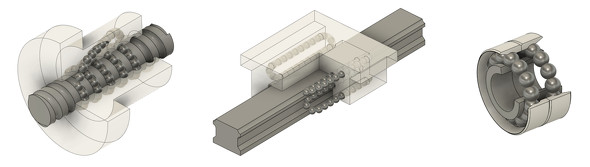
図11にボールねじ、LMガイド、アンギュラベアリングを示します。これらの共通点はボールが組み込まれているところです。
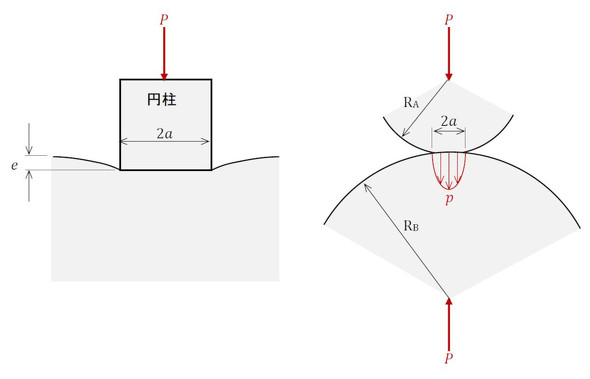
ボールが組み込まれることで、1軸アクチュエーターの剛性はどうなるでしょうか。“ボールがある”ということは、部品間の接触は球と曲面の点接触です。点接触では接触面積が極端に小さくなっているため、局所的な面圧が大きくなり、簡単に陥没すること、つまり接触剛性(ばね定数)があまり大きくないことが予測されます。どの程度か試算します。図12に示すように、円柱と平面の接触と、2球の接触を比較します。
円柱と平面の接触は、剛体パンチの接触となり、円柱は剛体です。陥没量eと加圧力Pは次式の関係があります(参考文献[2])。
ばね定数を次式で定義します。
2球の接触は「ヘルツの接触理論」を使います。2球の接近量δと加圧力Pは次式の関係があります(参考文献[2])。
今回は球と平面の接触なのでRBは無限大とします。式3には球自身の弾性変形は含まれていないようです。ばね定数を次式で定義します。
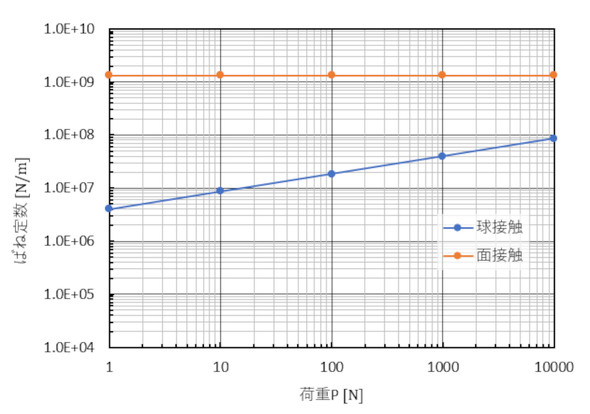
円柱と平面の接触を普通の部品の接触(面接触)、2球の接触をボールねじ内の接触(点接触)と考えます。鉄鋼材料の材料定数を使い半径を3[mm]としたばね定数を計算したものを図13に示します。
ボールねじ内のボールの数は30個くらいでしょうか。30個で3000[N]の軸力を発生させるとすると(フレーキングが起こりそうですね)荷重Pは100[N]です。このときの両者のばね定数は約2桁違います。ボールを使った接触にすると、ばね定数が約100分の1になるということでしょうか。ボールねじやLMガイドのカタログに目を通してみると、ゴツゴツとした剛性の高いもののように見えますが、実は点接触なので剛性は見た目よりもかなり低くなります。
参考文献:
- [2]日本機械学会|機械工学便覧 A4 材料力学(1992)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 幾何公差の基準「データム」を理解しよう

 式1
式1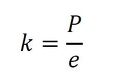 式2
式2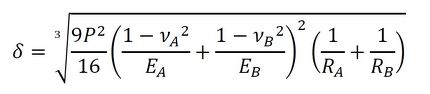 式3
式3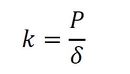 式4
式4