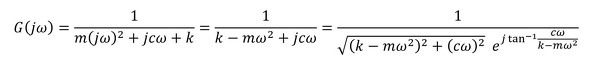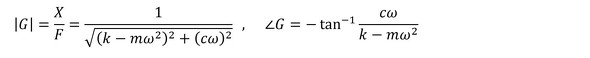振動低減の戦略 〜ばね−マス系の振動【1】〜:CAEと計測技術を使った振動・騒音対策(8)(2/5 ページ)
比例粘性減衰を持つばね−マス系
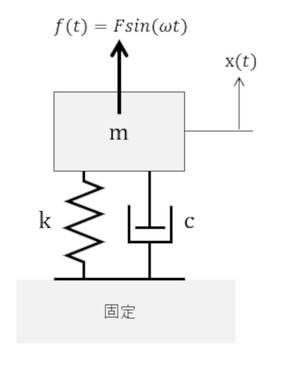
図4に示すように、質量mの物体にF sin(ωt)なる力が作用している場合を考えます。質量mの物体を「質点」と呼ぶことにします。ω[rad/s]は、角振動数で周波数をf[Hz]とすると、ω=2πfです。物体は床に対してばねで固定されています。ばね定数はk[N/m]とします。次に、物体には抵抗力が作用しているとします。そして、この抵抗力は物体速度に比例するとします。このような抵抗によって運動は減衰されるのですが、この減衰は「比例粘性減衰」と呼ばれています。物体に作用する力は以下の3つとなります。
運動方程式は次式となります。
抵抗力については、速度に比例する量としました。こうすると簡単に微分方程式が解けます。しかし、われわれが日常遭遇している摩擦力はクーロン摩擦であって、摩擦面に作用している力に比例する量でした。つまり、変位xには関係なく一定値で、その方向は運動方向と逆方向です。つまり、方程式の符号がxの時間微分によって反転します。こうなると途端に微分方程式が解けなくなります。その結果、シミュレーションをすることになり、いずれ紹介しますが接触要素を使ったフル法の時刻歴応答解析を行うことになります。フル法の時刻歴応答解析は、普通の応力解析の200倍以上の計算時間がかかります。
次に、われわれが感じる空気抵抗はほとんどが乱流場なので速度の二乗に比例します。式3を変えなければなりませんし、符号がxの時間微分によって反転します。この場合も微分方程式を解くのが難しくなります。比例粘性減衰というのは、ばね−マス系を簡単に説明するための便利な抵抗であって、比例粘性減衰とは程遠い現象をわれわれは向き合っている場合があることを意識しておいてください。
微分方程式を解きましょう。式5の右辺をゼロとした斉次方程式の一般解と式5の特殊解の和が式5の一般解でしたね。次式となります。
式6第1項が斉次方程式の一般解で、場合分けして3通りの形がありますが、そのうちの1つを記載しています。式6第1項にe-ζtが付いているので時間の経過とともに小さくなります。式6第2項が式5の特殊解で角振動数ωは外力の振動数です。「OpenModelica」(参考文献[1])を使って式5を解いてみました。図5左図に示します。図5左図の1.5[s]以降は単純なsin波なので、その周波数と振幅を読み取ってsin波にしたものを図5右図に示します。図5左図から図5右図を引き算したものを図5中央図に示します。これで、運動方程式の解を自由運動の解と強制振動の解に分解したことになります。運動方程式の解は、斉次方程式の一般解と特殊解の和だったのですが、これに相当します。
自由運動の解は時間の経過とともに減衰するので見ないことにして、強制振動の解だけに注目します。強制振動の解はsin波なので、質点の物体の変位は次式であると考えます。
Xが振幅、Φはマイナス値となるので位相遅れとなります。式7を式5に代入します。
sinとcosの和なので次式を使うと、式8は式10となります。
sinの係数とかっこ内が等しいとすると、次式が出来上がります。
伝達関数Gは「変位/力」で、「複素数で表示するか」あるいは「振幅と位相角で表示するか」でした。後者での検討をオススメします。伝達関数の振幅と位相角は次式となります。
伝達関数が求まりました。別の方法で伝達関数を求めます。運動方程式(式5)をラプラス変換すると次式になります。
伝達関数は次式となります。
伝達関数を振幅と位相角で表現するためには、sにjωを代入すれば求まります。次式となります。
式12と同じ形になりました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

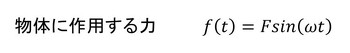 式1
式1 式2
式2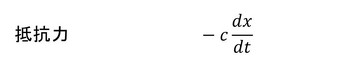 式3
式3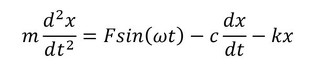 式4
式4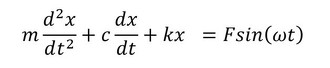 式5
式5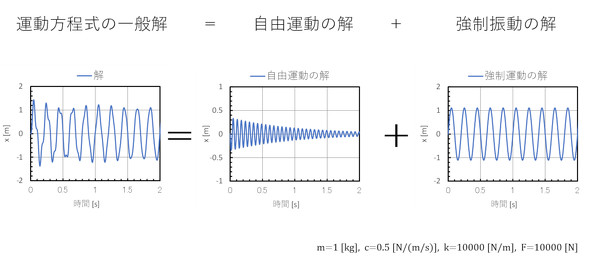
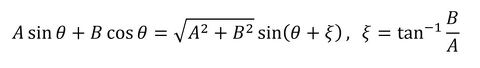 式9
式9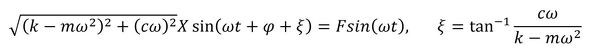 式10
式10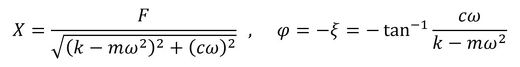 式11
式11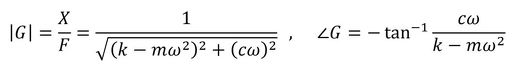 式12
式12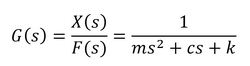 式14
式14