振動低減の戦略 〜ばね−マス系の振動【1】〜:CAEと計測技術を使った振動・騒音対策(8)(4/5 ページ)
「振動数が一致していないが共振に近い」ときのアクション
「振動数が一致していないが共振に近い」ときや「加振源の周波数と機械の固有振動数は全く異なるが振動が大きい」ときはどうすればよく、対策の効果をどのように見積もればよいでしょうか。前述したばね−マス系の伝達関数を使って説明しましょう。
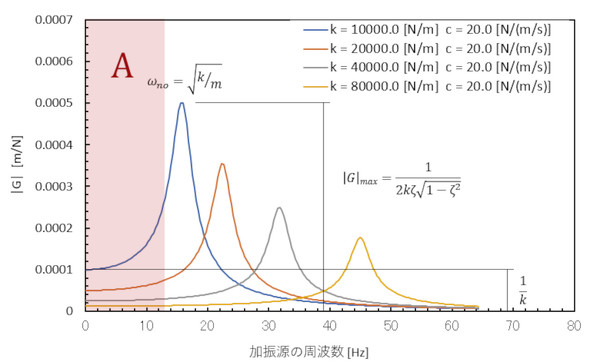
ばね定数をいろいろと変えて伝達関数の振幅を計算したものを図9に示します。加振源の周波数が機械の固有振動数よりも低い場合を考えます。図9はばね定数をいろいろと変えてみた場合ですが、ばね定数を大きくすると伝達関数が見る見る下がっていきます。ここで述べるのは、図9の領域Aの場合で、機械の固有振動数よりも加振源の固有振動数が高いときです。
式12は以下でした。
振幅Xは次式となり、加振力の振幅が変わらなければ、振幅Xは伝達関数の絶対値|G|に比例します。
式20の分母にばね定数kがあるので、kが倍になると伝達関数は半分になり、振幅も半分になるという発想です。機械の剛性は高ければ高いほど振動低減にとって有利なことが分かります。振動対策は以下のアクションが有効です。
機械のばね定数、つまり剛性を上げる
かなり乱暴で誰でも気が付くことを書きました。実際の機械の伝達関数には、ばね−マス系のように共振点が1つではなくたくさんあって、たくさんあるピークの山と山の間に加振力の周波数を移動すれば……との発想が思い浮かびます。しかし、そのように器用なことは筆者にできるはずもなく、剛性を上げる手段をよく使っていました。特殊な振動対策をするよりもシンプルで分かりやすいですね。
機械の剛性を高くするためにはどうすればよいでしょうか。剛性を高くすると、機械の固有振動数も高くなるので、筆者がよく使っていた固有振動数を求める式を紹介します。
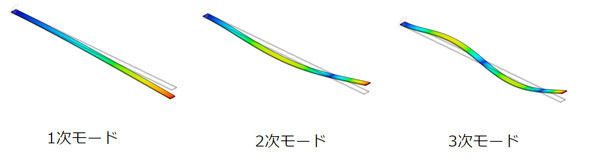
機械が弾性変形するときは、棒が引っ張られて変形する量よりも、はりの曲げで変形する量の方がはるかに大きい場合が多いので、片持ちはりの固有振動数の式を使います。片持ちはりを図10に示します。片持ちはりの振動の共振点はいくつかあって(厳密には無限にあって)、振動数の低い共振点の振動形状を図11に示します。
このような形に振動することは避けられないので、このときの振動数、つまり固有振動数を上げる戦略をとります。固有振動数は式28で求めることができます。
断面二次モーメントは次式でした。
式28の分母にl2があるので、はりの全長を短くすると固有振動数は劇的に上昇して、振動面で有利となります。機械を設計するとき、細長い部品には注意が必要となります。断面二次モーメントは板厚の3乗に比例するので薄い板厚部にも注意が必要で、全長や板厚を変更するという案が浮上します。材質を変えるという案は、ヤング率が大きくなって、かつ密度が下がるような材質だと効果がありますが、ヤング率だけが大きくなってもヤング率のルートに比例するだけなので、あまり効果は期待できません。
板厚を厚くすると重くなって、式19から固有振動数が下がってしまうので、式28を変更します。式30となります。
結局、固有振動数は板厚に比例するということになりました。しかし、重量、つまり断面積を変えずに断面二次モーメントを上げる策はいろいろとあるので、断面二次モーメントの操作が振動対策に有効となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本

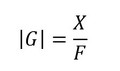 式26
式26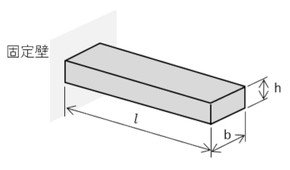
 式28
式28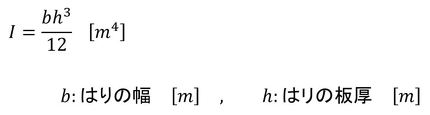 式29
式29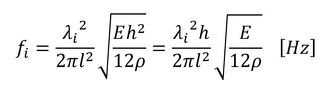 式30
式30





