振動低減の戦略 〜ばね−マス系の振動【1】〜:CAEと計測技術を使った振動・騒音対策(8)(3/5 ページ)
伝達関数をグラフで表現する
もう少しお付き合いください。限界減衰co、減衰比ζ、無減衰固有角振動数ωno、無減衰固有振動数fnoを導入します。次式で定義されます。
限界減衰coの意味するところは、図5の自由運動の解が2通りあって、図6に示すように比例粘性係数cがcoより小さいと、つまり減衰力が小さいと自由運動の解は振動するのですが(図6左図)、cがcoより大きいと、つまり減衰力が大きいと自由運動の解は一度も往復運動せずにゼロに近づきます(図6右図)。coは図6左図になるか図6右図になるかの境目の比例粘性抵抗です。
式17、18、19を式12に代入すると次式になります。
共振点、つまり固有振動数は式20で計算されることが多いのですが、減衰があると少しずれます。式21の値が最大となる角振動数が共振点となり、式21のルートの中を微分することで共振点の角振動数が求まります。次式となります。
伝達関数の最大値は、式23を式20に代入することで求まり、次式となります。分母にばね定数kと減衰比ζがあることに注目してください。
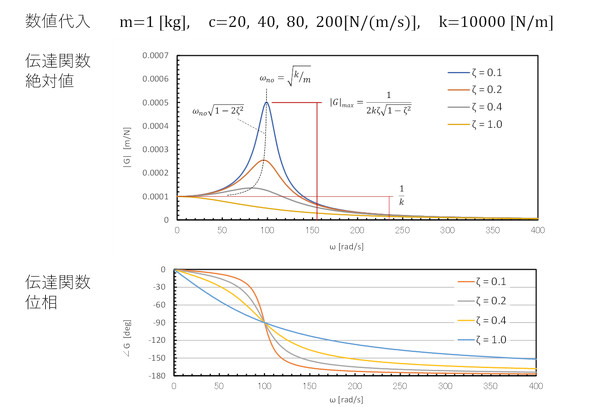
数値を代入した例を図7に示します。位相角ですが、アークタンジェントの戻り値は+90〜−90[deg]なのですが、外力に対する応答が外力よりも早い時間に起こることはあり得ず、応答は常に遅れるので、0〜+90[deg]のときは180[deg]だけ引き算しています。文献でよく見掛けるグラフになりました。
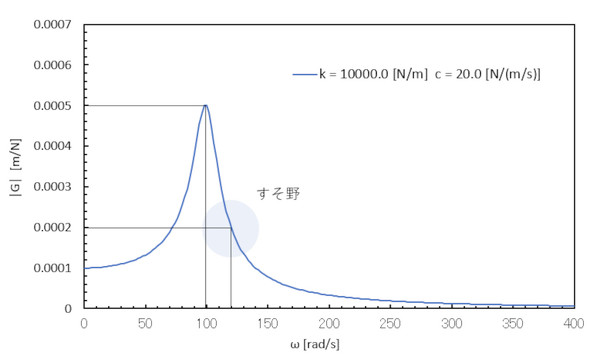
伝達関数の裾野について
周波数分析について説明した際、「ピーク値近傍の裾野の値は単にsinとcosを掛算した総和であって、信号には含まれない」といった旨のお話をしました。しかし、ばね−マス系の伝達関数の裾野には意味があります。図8に示すように、このばね−マス系を120[rad/s]で加振したときの振幅の伝達関数は0.0002[m/N]であって、振幅1[N]で加振したら変位の振幅は0.0002[m]となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

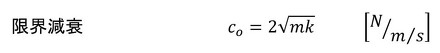 式17
式17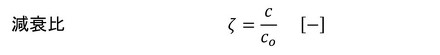 式18
式18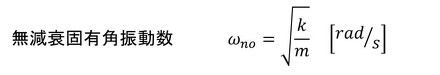 式19
式19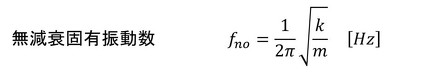 式20
式20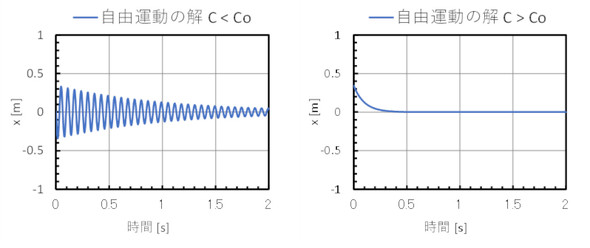
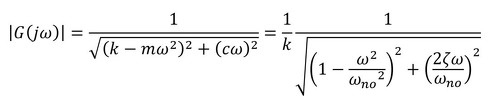 式21
式21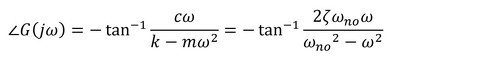 式22
式22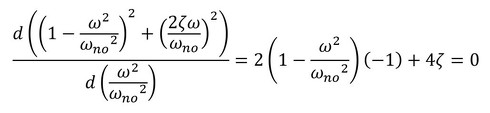 式23
式23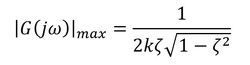 式25
式25