「1Dモデリング」に関する連載。連載第19回は“エレベーターの乗り心地のモデリング”を取り上げる。振動と乗り心地の関係について述べ、続いてエレベーターの仕組みと振動、ひとの振動検知部位とひとのモデリングの方法を説明し、最後にエレベーターの乗り心地のモデリングを行い、解析結果から、ひとにより乗り心地が異なることを示す。

» 2023年05月17日 09時00分公開

[大富浩一／日本機械学会設計研究会，MONOist]

　前回、ひとのモデリングの考え方とその方法について述べた。今回は、その適用例の1つとして“エレベーターの乗り心地のモデリング”を取り上げる。

　エレベーターなどの移動交通機器に乗った際、ひとはその動きを感じ、ある場合には気にならなかったり、また場合によっては不快に感じたりする。ここでは、これを“乗り心地”と定義する。

　乗り心地は、当然エレベーターなどの機器が起因となっているため、これらの“もののモデリング”は不可欠であるが、これらが発生する振動を感じるのは“ひと”であり、この部分は“ひとのモデリング”を必要とする。

　そこで、最初に振動と乗り心地の関係について述べ、続いてエレベーターの仕組みと振動、ひとの振動検知部位とひとのモデリングの方法を説明し、最後にエレベーターの乗り心地のモデリングを行い、この解析結果から、ひとにより乗り心地が異なることを示す。

⇒連載バックナンバーはこちら

表記について：

※1）「もの」「モノ」の表記について：本稿では、生産活動によって付加価値が与えられた成果物を表す場合は「もの」、経営学の三要素「ヒト、モノ、カネ」のように生産要素やリソースとして表す場合は「モノ」と表現する。

※2）「人」「ヒト」「ひと」の表記について：本稿では、「人：一般的」「ヒト：生物学的」「ひと：人間的（ものとの対比）」と使い分けて表記している。

振動と乗り心地

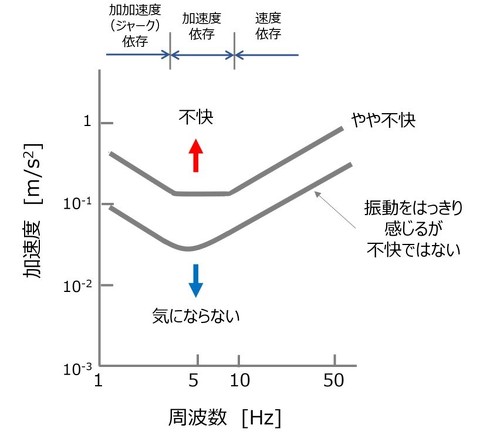
　乗り心地に関しては、クルマを中心に多くの研究がなされていて、規格化されている場合もある。図1に「Meisterの振動感覚曲線」（参考文献［1］）を示す。入力として縦軸に加速度、横軸にその周波数を取り、ひとの感覚を出力として曲線で示している。

図1　Meisterの振動感覚曲線［クリックで拡大］

　図1では“やや不快”と“振動をはっきり感じるが不快ではない”の2つの線（オリジナルでは6つの線が示されている）を示している。ここから、乗り心地の限界曲線はこの2つの線の間にあると考えられる。すなわち、5Hzの入力に対してひとは最も敏感であることを示している。この要因はさまざまであるが、1つにはひとが一種の振動系を構成しており、ひとの共振点が5Hzに存在すると考えられる。最も単純なケースとして、ひとを一自由度のMCK（マス、減衰、ばね）モデルで考え、図の限界曲線に合致させるには、減衰比を0.2にすると都合がいい（参考文献［1］）といわれている。また、図1から、ひとは3Hz付近までは加加速度（ジャーク）、5Hz前後では加速度、それ以上では速度に対して、乗り心地を敏感に感じていることが分かる。

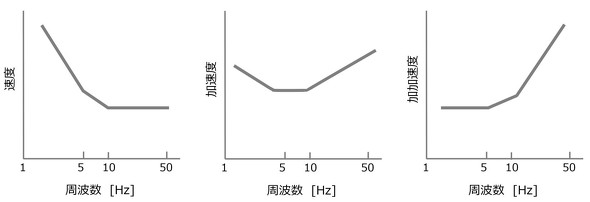
　もう少し分かりやすく説明すると、図1の振動感覚曲線について、縦軸を速度、加速度、加加速度で表現すると図2となる。これから、比較的高い周波数を対象とする一般の機械振動（電動工具など）では、振動速度を基本に規格化されている理由が理解できる。一方、エレベーターやクルマなどにおいては、その動きが低周波であるため、加速度および加加速度も重要な評価因子となる。