Excelを使って周波数分析をやってみよう!:CAEと計測技術を使った振動・騒音対策(5)(3/5 ページ)
マクロ付きExcelで周波数分析(続き)
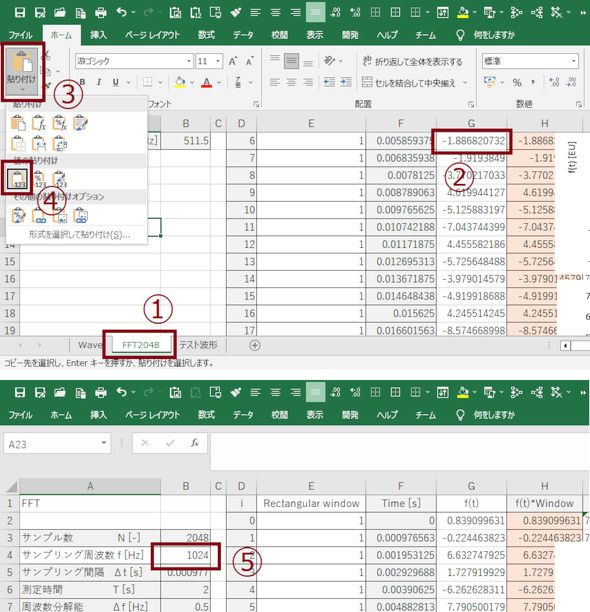
次に、図10に示すように(1)「FFT2048」シートに移動し、(2)G1セルを選択して、(3)[形式を選択して貼り付け]をクリックして、(4)[値の貼り付け]ボタンを押します。そして、(5)サンプリング周波数を1024[Hz]とします。
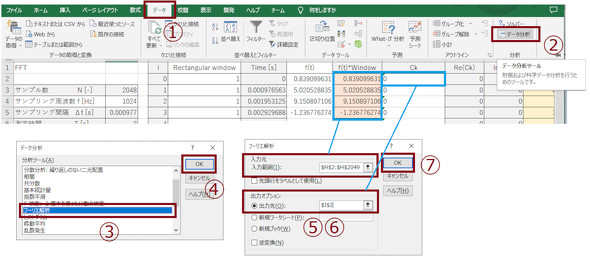
さらに、図11に示した通り、(1)メニューの[データ]をクリックし、(2)[データ分析]を選択するとデータ分析ウィンドウが表示されるので、(3)[フーリエ解析]を選んで、(4)[OK]ボタンを押します。すると、フーリエ解析ウィンドウが表示されるので、(5)(6)図の通りに入力範囲($H$2:$H$2049)と出力先($I$2)の値を入力して、(7)[OK]ボタンを押下します。入力範囲(H列)は「テスト波形」シートで作成したデータ列に、後述するウィンドウ関数を掛け算したものです。ここではウィンドウ関数の値は1です。
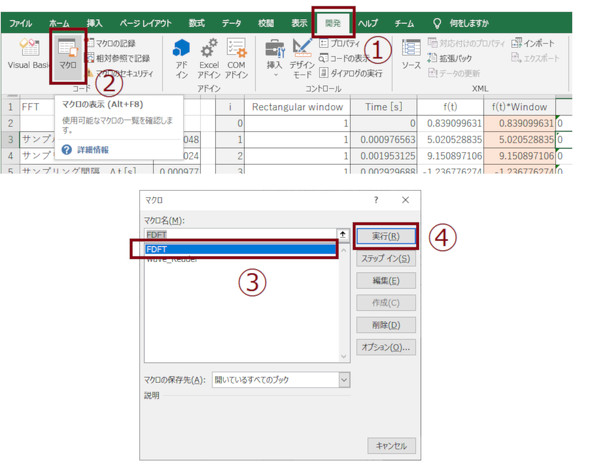
図12に示した手順でマクロプログラムを実行しても、これらと同じ操作をしたことになります。
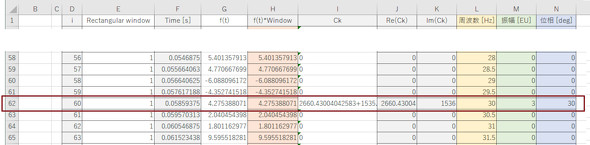
では、離散フーリエ変換の結果を見てみましょう。「FFT2048」シートの62行目にある60番目の離散フーリエ変換結果は複素数で、以下の値となります。
実部が2660.43、虚数部が1536.00ですね。式10から60番目のデータの周波数は次式の値となります。
Excelの離散フーリエ変換は連載第4回の離散フーリエ変換の式(式12と式13)におけるN分の1倍をしていないので、Excelシートの中でN分の1倍します。式3の周波数成分の振幅は式5を使うと次式で求まります(式13)。
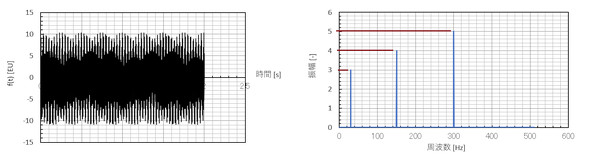
Excelシートの62行目を図13に示します。テスト波形を作ったときに30[Hz]成分の振幅を3にしたので、離散フーリエ変換結果も振幅が3になりました。
図14に元波形と離散フーリエ変換結果を示します。同様に150[Hz](302行目)と300[Hz](306行目)の振幅も求まっています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

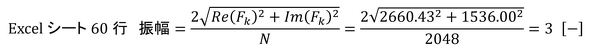 式13
式13