振動・騒音対策の前に「周波数分析」の必要性と原理を理解する:CAEと計測技術を使った振動・騒音対策(4)(1/4 ページ)
連載「CAEと計測技術を使った振動・騒音対策」では、“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた機械の振動対策と騒音対策の考え方や、その手順について詳しく解説する。連載第3回では「周波数分析」について取り上げる。
振動や音圧波形は時間とともに変化するので、その波形のグラフの横軸は時間軸ですが、振動対策と騒音対策では横軸を周波数として取り扱うことが常とう手段となります。横軸を周波数軸とした取り扱いに慣れましょう。
今回は「周波数分析」について取り上げます。ちなみに、本連載の主題である“振動・騒音対策”は周波数分析をご理解された後のお話になります。
なぜ、騒音波形の横軸を周波数軸にすべきなのか
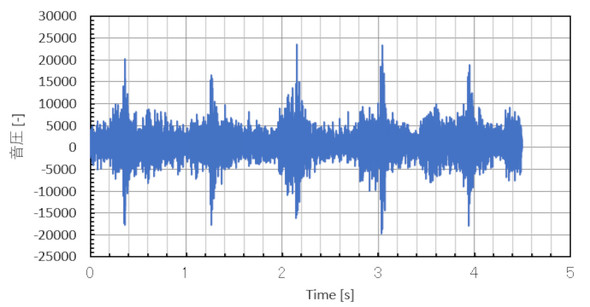
図1はある部品を打ち抜くプレスの近傍で測定した音圧データです。縦軸は符号付き16ビット整数型変数の値で、音圧に比例した−3万2768〜3万2767の数値で、横軸は時間です。これを見て対策を立てようとしてもなかなかアイデアは出ませんね。
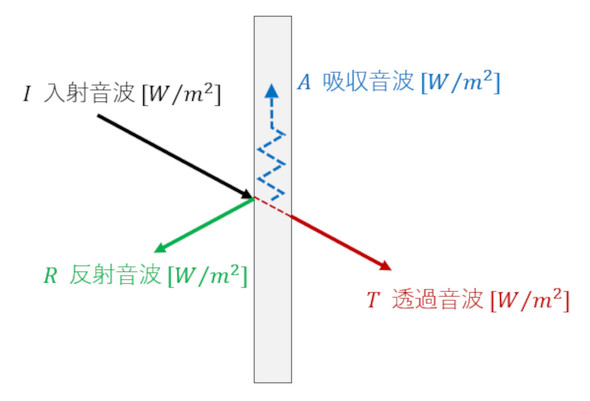
図2に音波の壁での透過と反射を示します。壁によって音が遮られて音が小さくなります。つまり、透過音波Tは入射音波Iよりも小さくなります。また、壁で音が反射します。
式1で定義される量は「透過損失」と呼び、この値が大きければ大きいほど壁によって遮られた騒音は小さくなります。透過損失の数値例を図3に示します。透過損失は壁の単位面積当たりの質量で決まりますが、詳しくは本連載の後半で説明します。厚さ1[mm]の鋼板では、1000[Hz]の音を約30[dB]下げるのですから、この壁(「遮音壁」と呼びます)を使わない手はありません。
よく響く部屋の音が大きいことは読者の皆さんも経験されていると思います。壁からの反射音が大きければ大きいほど部屋の音が大きくなるので、壁からの反射を小さくすると部屋全体の騒音を下げることができます。このために、壁に吸音材を貼り付けます。壁からの反射音の度合いを「吸音率」といい、少し大ざっぱですが次式で定義されています(式2)。吸音率の数値例を図4に示します。吸音率には「垂直入射吸音率」「ランダム入射吸音率」「残響室法吸音率」がありますが、これらについても本連載の後半で説明します。
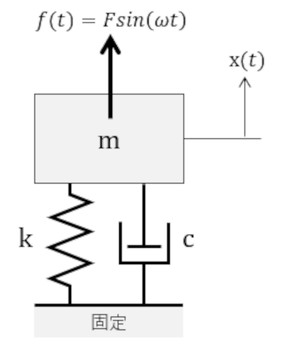
図5に、質量mのおもりが床にばねとダッシュポットでつながれていて、おもりにFsin(ωt)の外力が作用している状態を示します。ωは角振動数[rad/s]で、周波数をf[Hz]とすると、ω=2πfです。おもりの変位をx(t)とし、その周波数分析結果をX(ω)とすると、伝達関数の周波数表示G(ω)は次式となり、X(ω)はF(ω)とG(ω)の積となります。
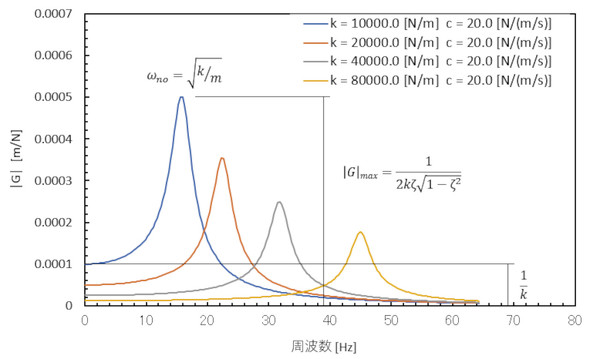
おもりの変位は外力に比例するのは当然として、伝達関数にも比例します。ということで、ばね定数kを変えたときの伝達関数を図6に示します。周波数が20[Hz]以下の伝達関数に注目します。ばね定数kを大きくすると伝達関数が見る見る低下することが分かります。ということは、振動変位も低減します。ばね−マス系についても本連載の中盤で説明します。
ここまで3つのグラフを紹介しました。全て横軸は周波数で表現していました。つまり、周波数が分からないと対策の効果量が予測できません。よって、図1の騒音波形も横軸を周波数軸として表現する必要があります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

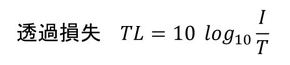 式1
式1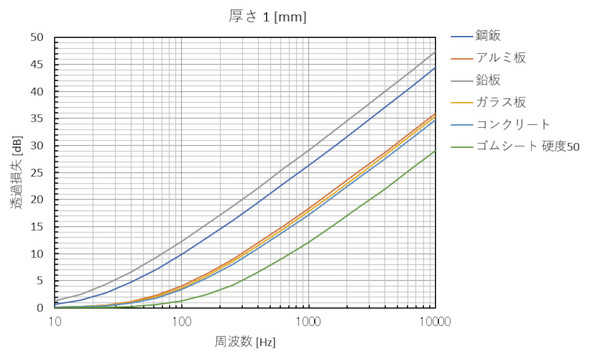
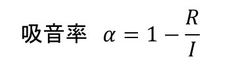 式2
式2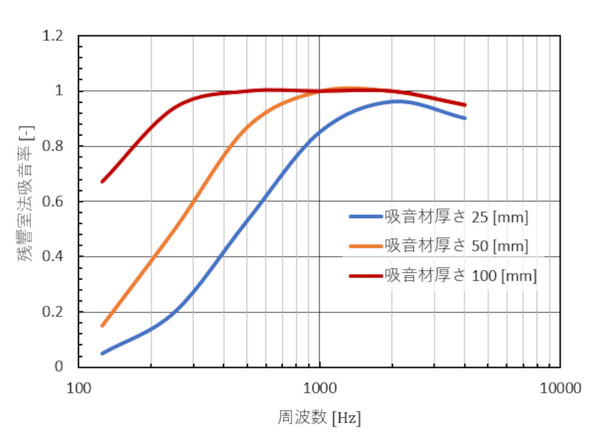
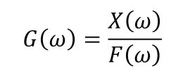 式3
式3