密度法によるトポロジー最適化の準備を行う:フリーFEMソフトとExcelマクロで形状最適化(6)(2/6 ページ)
最適性規準法の続き
図1の*Bで示した「Dが1に近づくようにρiを更新」の方法を説明します。λがマイナス値であることを意識して式6を眺めてみましょう。有限要素法解析の結果、ある要素の応力が大きな値であったとします。式6の分母が大きくなり、Dを1に近づけるにはρiを大きくしなければなりません。反対に要素の応力が小さな値のときはρiを小さくしなければなりません。参考文献[1]は密度法ではなく「均質化法」なのですが、次の世代のρiを求める式があります。しかし、ρiの変化量が大き過ぎると反復計算が発散するのでρiの変化量にリミッターをかけています。ほとんどの場合、リミッターに引っ掛かりますので、リミッターの数値をρiの変化量とします。次式でρiを更新します。
もう1つリミッターをかけます。ρiは1以上にはなれず、かつマイナス値にもなれません。次式となります。
この辺りは「Excel」のマクロプログラムに仕込んでおらず、シートのセルに式として設定しています。任意に数値やアルゴリズムを変えられると思います。
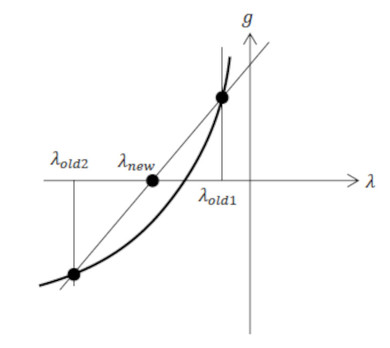
図1の*Cで示した「λを更新」の方法を説明します。式7が成立するようなλを求めます。式7を眺めると、ρiが大きくなれば、gも大きくなります。図2左図のようになります。
次に式5が1と等しいとして、その式を変形します(式14)。
λとρiの関係は、nが2か3で、マイナスの反比例です。図2中央図のようになります。そうすると、gとλの関係は図2右図になるのでしょうか。
式7、つまりg=0が目標です。図2右図から、gがマイナスのときはλを増やし、gがプラスのときはλを減らせばよいということになります。次式でλを更新します。
前述の操作でgの符号が反転すればしめたものです。以降は図3のように、1次式で新しいλを求めて、g/Voが許容値(1%で十分です)以下になれば、λが求まったことになります。あと1つ、ρiは0.05[-]刻みで変化するので、λを変えてもgが変化しなくなることがあります。よって、gが変化しなくなったらλが求まったことにして、図1の内側の反復計算を終了します。
図1の*Dで示した「各ρiが0ないし1になったか」の判定と計算終了の判断は人間が行います。図4に最適化した例を示します。グレーの領域があります。全ての要素のρiが完全に0か1になるまで計算を続けると、大切な小骨がなくなってしまいます。最後の判断は人間で行いましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

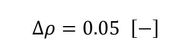 式10
式10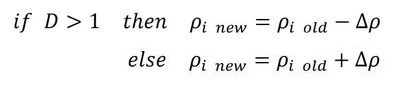 式11
式11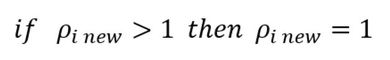 式12
式12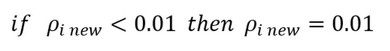 式13
式13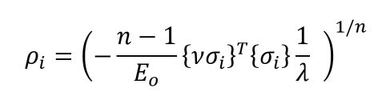 式14
式14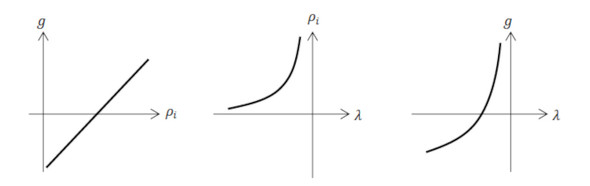
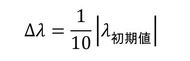 式15
式15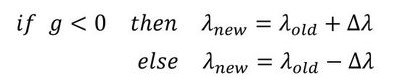 式16
式16