密度法によるトポロジー最適化の準備を行う:フリーFEMソフトとExcelマクロで形状最適化(6)(1/6 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第6回では「最適性規準法」を用いて、剛性を最大化=平均コンプライアンスを最小化する設計パラメータを求める。
これまで式の導出が続きましたが、いよいよ最適化アルゴリズムの本丸です。「最適性規準法(Optimality Criteria法)」(参考文献[1][2])」を使って、剛性を最大化=(イコール)平均コンプライアンスを最小化する設計パラメータρiを求めましょう。
最適性規準法
ラグランジュ関数Lは以下の式でした(式1)。
これをρiで微分したものが0です。
では、最適性規準法を用いて式2を満足させるρiを求めます。式2を式3のように変形します。
両辺を∂f/∂ρiで割ります(式4)。
そして、連載第5回の結果を代入します(式5)。
スカスカ状態の見掛けの体積はVoで、真の体積はaVoでした。設計パラメータである密度ρiの平均値は、ρiの定義からaと等しくなります。これから反復計算をしますが、ρiの初期値はaとなります。ρiは最終的な解ではないので式5は成立しません。次式のように変数Dを導入します(式6)。
式1をλで微分したものも0でした。次式となります(式7)。
計算していくと分かることなのですが、λも未知数で反復計算して求めます。反復計算の最中はλの変化に従って、ρiも変化します。よって、式7においてはρiをλの関数として表現しました。
計算手順を図1に示します。2重ループになっています。
図1の*Aで示した「λの初期値を設定」について説明します。式6において分子にヤング率Eoがあり、鋼の場合Eo=200×109[Pa]です。分母は応力の2乗です。式6のDを1に近づけるためのλは、109のオーダーか、1桁台か、10−9のオーダーか見当がつきません。λを反復計算で求めるのですが、やみくもな値を初期値にすると答えが得られません。そこで、以下の発想でλの初期値を決めました。
式3を変形し、連載第5回の結果を代入します(式8)。
i=1、2、3……neと、ne通りのλがあります。これらの平均値をλの初期値としましょう。式9です。λがマイナス値になることは「密度法」ではお約束です。
式9の出番は図1の大きなループの1回目だけです。2回目以降は前回求まったλを初期値にします。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

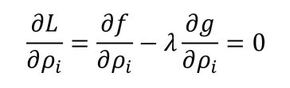 式2
式2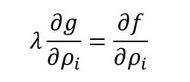 式3
式3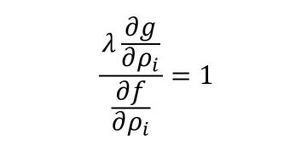 式4
式4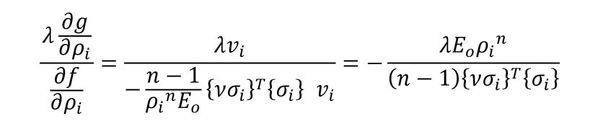 式5
式5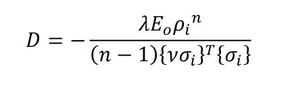 式6
式6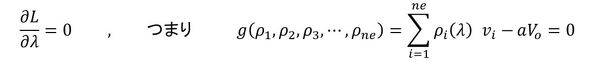 式7
式7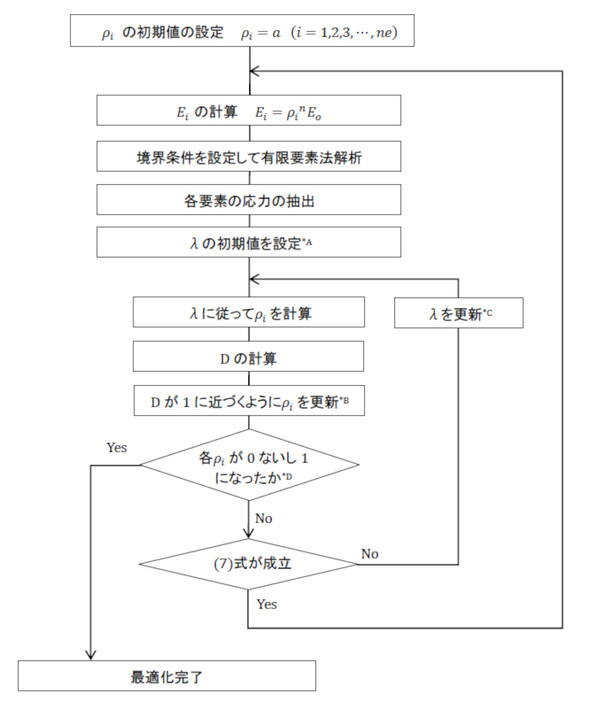
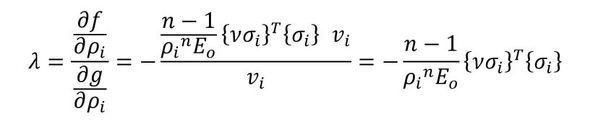 式8
式8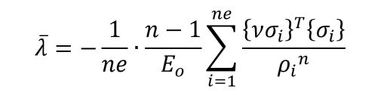 式9
式9





