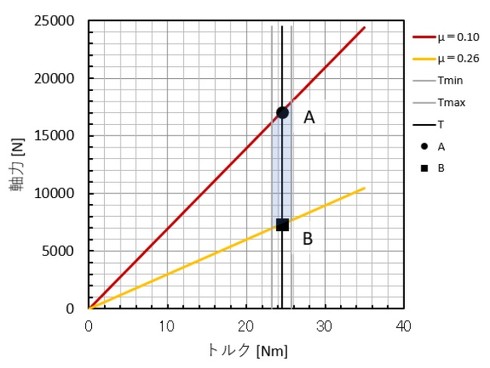
　トルク係数が求まっているので、M10の場合の締め付けトルクと軸力の関係を図9に示します。グラフの傾きは「1／（呼び径×トルク係数）」です。締め付けトルクを被締結体（ないしはナット）の材質ごとに別々に決めるのではなく、いろいろな材質の被締結体に対応できるようにするために、摩擦係数のばらつき（0.10～0.26）も考慮する必要があります。また、締め付けトルクがT_min～T_maxまでばらつくとすると、軸力は図9の着色した範囲内（薄い水色の範囲内）でばらつくことになります。締め付け係数Qは通常1.4ですが、今回は2以上になってしまいました。

図9　締め付けトルクと軸力の関係 M10 ［クリックで拡大］

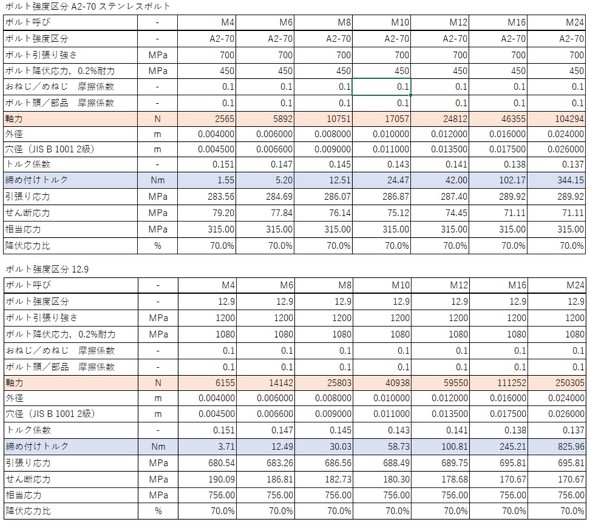
　締め付けトルクは相当応力が最も大きくなる条件、つまり軸力が最も大きい条件で決めるべきなので、図7のA点となります。式4によるとボルト軸力計算式の分母に摩擦係数があるので、摩擦係数はばらつきの中の最小値を選択することになり、摩擦係数として0.10［-］を採用することにします。A2-70のステンレスボルトと強度区分12.9のボルトについて、Excelのゴールシークを使って降伏応力比がちょうど70％になるような締め付けトルクを求めました。これが締め付けトルクとなり表4に示した値となります。

表4　ボルト締め付けトルク［クリックで拡大］

T系列と2.4T系列について

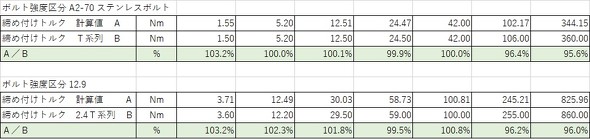
　T系列（参考文献［4］）は強度区分4.6～6.8のボルトやステンレスボルトに対する締め付けトルクです。2.4T系列は強度区分10.9～12.9のボルトに対する締め付けトルクです。ここで計算した締め付けトルクとT系列、2.4T系列との比較を表5に示します。両者の比は95～105％の間に入り、ほぼ一致しています。つまり、T系列や2.4T系列は、締め付けたときの降伏応力比が76～84％になるような締め付けトルクということになります。これで冒頭で述べた「締め付けトルクは？」の問いに答えられると思います。