ボルトの締め付けトルクを決める:設計者向けCAEを使ったボルト締結部の設計(6)(2/5 ページ)
ボルトに発生する相当応力
ボルトに発生する相当応力が、降伏応力ないしは耐力の何%かを計算するため、相当応力を求めましょう。連載第4回で締め付けトルクと軸力の関係を導きました。そのときの式を使います。ボルトに作用する軸力、つまり引張力Fは式4で表されます。
JIS B 1083によると、Dbは次式で計算します(式5)。
ボルトを円柱と考えて応力を求めます。円柱の断面積を「有効断面積」と呼び、Asとします。有効断面積に相当する直径、つまり円柱の直径をdASとします。dASとAsは次式で求めます(式6、式7)。
引張力Fを有効断面積で割れば、応力集中を考慮しない平均的な引張応力が求まります(式8)。
では、せん断応力τを求めましょう。連載第4回で求めた締め付けトルクと軸力の関係は次式でした(式9)。
式9の第1項はねじ山で発生する摩擦トルクTth、第2項は軸力を発生させるためのトルクTa、第3項はねじの頭と被締結体で発生する摩擦トルクTbです。ボルトの軸部に作用しているトルクTsは、第1項と第2項の和となります(式10)。
円柱のねじり断面係数Zpは次式です(式11)。
せん断応力は式12で計算できます。
式8の結果と式12の結果を式3に代入すれば、谷底の応力集中を考慮しないボルトに発生する相当応力が求まります。
締め付けたときの相当応力と降伏応力(または耐力)の比を「降伏応力比」と呼ぶことにしましょう。降伏応力比は次式で定義されます(式13)。
式13を使って、降伏応力比が70%となるような締め付けトルクを決めればよいことになります。ここで降伏している領域を考えてみましょう。式12で求まるせん断応力は、円柱の外表面の応力です。降伏応力比が100%の場合、降伏している領域は図3左図(旧JIS)の赤色で示したように円柱の外表面です。これではほとんどの領域が降伏していません。塑性締め付けが広く採用されるようになったので、塑性変形に対してもう少し寛容になってもよいかと考えられます。
2008年にJIS B 1083「ねじ締め付け通則」が改訂されました(参考文献[3])。ボルトの降伏条件が、「円柱の外表面が降伏応力になっているかどうか」から「円柱全域が降伏応力になっているかどうか」に変わりました。降伏領域は図3右図(新JIS)のようになります。新しいJISでは、せん断応力分布について少し強引な仮定をしています。
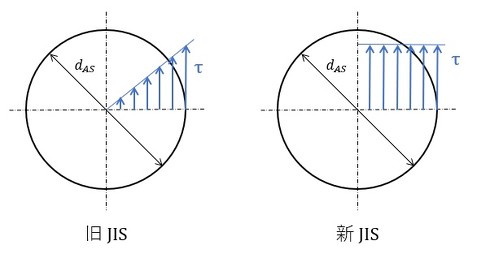
せん断応力分布を図4に示します。材料力学では、円柱をねじったときの応力分布は図4左図(旧JIS)のように半径座標に比例した量になります。一方、新JISではせん断応力が全て降伏応力になったと考えて図4右図(新JIS)のような分布としています。弾性領域がなくかつ加工硬化もないので完全剛塑性体です。
図4右図の場合のせん断応力とトルクの関係は、式14で計算できます。式12の代わりに式15を使ってボルトの応力を求めることにします。ねじ締結体の書籍には古いものがあり、式12を採用している可能性がありますが、新JISに従うことにしましょう。
参考文献:
- [3]日本規格協会:ねじ締め付け通則:JIS B 1083(2008)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
 式4
式4 式5
式5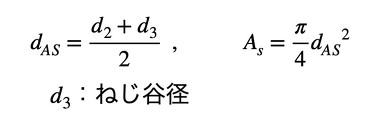 式6(左)、式7(右)
式6(左)、式7(右)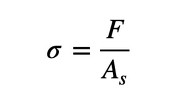 式8
式8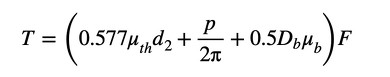 式9
式9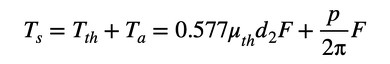 式10
式10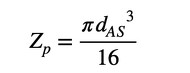 式11
式11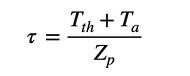 式12
式12 式13
式13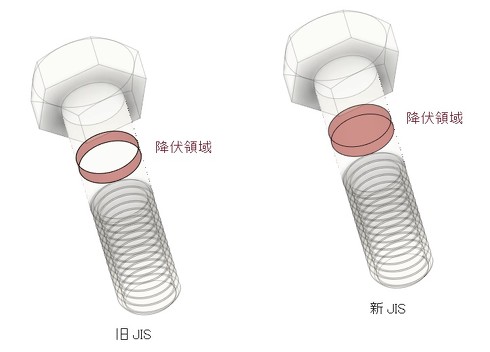
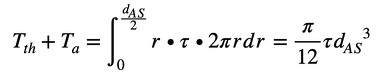 式14
式14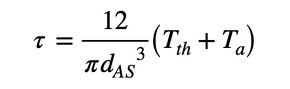 式15
式15





