ボルトの締め付けトルクを決める:設計者向けCAEを使ったボルト締結部の設計(6)(1/5 ページ)
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。これまでの連載で「締め付けトルクと軸力の関係」や「いろいろな金属の摩擦係数」が明らかとなったので、連載第6回ではボルトの締め付けトルクを決める。
連載第4回で締め付けトルクと軸力の関係、連載第5回でいろいろな金属の摩擦係数が明らかになりましたので、ボルトの締め付けトルクを決めましょう。
これで、デザインレビューや顧客からの「締め付けトルクは?」との問いに、「はい。今回はT系列を採用しましたが、これはいわゆる弾性締め付けで、締め付け時のボルトの相当応力が降伏応力の約70%になるような値としています」と言い切ることができます。また、T系列を使わずに自分で締め付けトルクを決めることも可能です。
なぜ降伏応力の約70%か
連載第3回で「ボルトが疲労破壊しない条件は、変動荷重が作用したときに締結体同士が離れないこと」と述べました。ということは、締め付け時の軸力が大きければ大きいほど疲労破壊しにくいといえるので、締め付けトルクを大きくしたいのです。これは緩み防止の観点からもいえます。
一方、普段の強度計算では、部品は塑性変形しないことを基準とするケースが多いので、上限は降伏応力となります。連載第5回で摩擦係数がばらつくことを話しました。摩擦係数がばらつくと同じトルクで締め付けても軸力がばらつき、ボルトに発生する応力もばらつきます。この対応として、ばらつきに対するマージンを30%とし、締め付け時のボルトに発生するミゼス相当応力を降伏応力の70%とすることが多いです。ちなみに「70%」という数値は多くの文献に載っていますが、1966年(昭和41年)に発行された「機械の研究」という雑誌の記事が、筆者が調べた中で最も古いものになります。
マージンを考慮して70%にしているということは、マージンを変えてもいいのです。ドイツではこれよりも大きな値が採用されているようです。
ボルトの締め付け管理方法
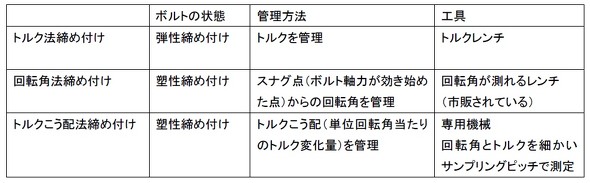
ボルトの締め付け管理方法は、大別して以下の3種類があります(表1)。
今まで話してこなかった「塑性締め付け」が出てきました。大きな軸力を発生させたいので、降伏応力の70%と言わずに、降伏応力全部を使ってしまおうという考え方です。軸力のばらつきを小さくできます。「回転角法締め付け」はバイクのメンテナンスなどでかなり普及しています(参考文献[1])。なお、塑性締め付けの場合、ボルトは再利用できませんので注意してください。
塑性締め付けが普及してきたので、弾性締め付けでの降伏応力の70%は、「70%以下」ではなく「70%くらい」と70%を超えてもよいと考えます。
ミゼス相当応力
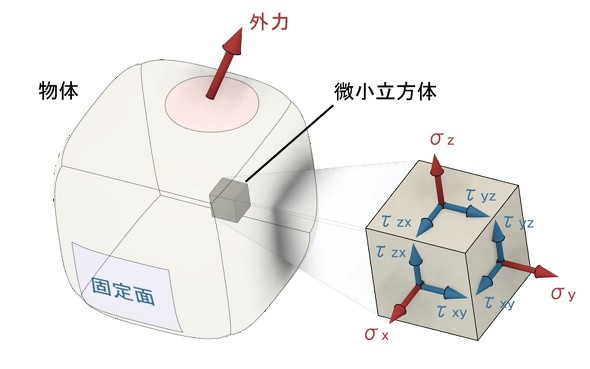
次に、金属材料が降伏したかどうかの判定方法を説明します。単純引張荷重の場合は、引張応力が降伏応力ないしは耐力を超えたら降伏していると判断できます。しかし、ボルトには図1に示すように、引張応力σと締め付けトルクによるせん断応力τが同時に発生しています。このような場合、どうすればよいのでしょうか。
図2に外力が働く物体の中の微小立方体に作用する応力を示します。微小立方体には、3つの垂直方向応力σx、σy、σzと、6つのせん断応力が作用しています。6つのせん断応力のうち、ペアが3組あるのでせん断応力の種類はτxy、τyz、τzxの3種類となります。微小立方体が降伏しているかどうかの判定に、せん断ひずみエネルギー説から導かれるミゼス相当応力を使います。ミゼス相当応力σeqは式1で計算されます(参考文献[2])。以降、ミゼス相当応力を単に「相当応力」と呼ぶことにします。
ボルトの場合は6つの応力成分のうち2つが発生しており、残りの4つはゼロです。次式となります(式2)。
式2を式1に代入すると、ボルトに作用する相当応力が求まります(式3)。
参考文献:
- [2]日本機械学会:機械工学便覧 A4 材料力学:P13(1992)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

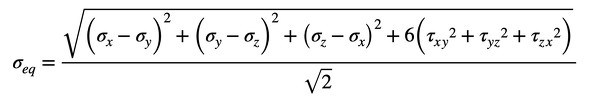 式1
式1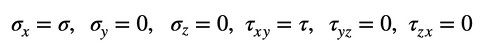 式2
式2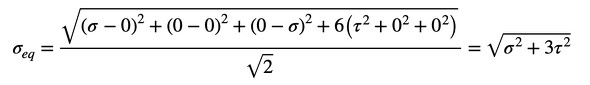 式3
式3





