AKB48……ではなくてODE45! FreeMatだと微分方程式が容易に解ける:無償ソフトで技術計算しよう【シミュレーション基礎編】(1)(3/3 ページ)
冷却の計算例
詳細は次回で説明するとして、(4)式で与えられる微分方程式をFreeMatで数値的に解いてみましょう。また、得られた結果と解析解(8)式で計算した結果とを比較してみます。
数値的に解くには、具体的な諸元が必要となります。ここでは、下記とします。直径5mm、長さ100mmで初期温度T0=100℃の鉄棒が、Ta=20℃の大気中にあります。鉄棒の物性値は、密度p=7800[kg/m3]、比熱c=470[J/kgK]表面熱伝達率a=10[W/(m2*K)]、とします。直径と長さから表面積はA=0.002[m2]、体積はV=1.963e-6[m3]となります。この鉄棒の初期から600秒間の温度変化を求めてみます。
下記のようにコマンドウィンドウに入力すると、図3の結果が得られます。
--> A=1.61e-3;V=1.963e-6;p=7800;c=470;
--> Ta=20;T0=100;a=10;
--> f=@(t,Te) -a*A*(Te-Ta)/(c*p*V);
--> [t,Te]=ode45(f,[0,600],T0);
--> Te2=Ta+(T0-Ta)*exp(-a*A*t/(c*p*V));
--> plot(t,Te,'+',t,Te2,'o'); grid('on');
--> xlabel('Time[s]');ylabel('Temperature[deg]');
図3は横軸が時間で縦軸が温度で、+は(4)式を数値的に解いた結果を、また、○は解析解の(8)式で計算した結果を示します。両者は良く一致していることが分かります。
入力内容を簡単に説明すると、1行目で表面積A、体積V、密度p、比熱cを、2行目で雰囲気温度Ta、初期温度T0と表面熱伝達率aを設定しています。
3行目で無名関数を使い、(4)式の微分方程式をfという名称で定義しています。4行目でfを初期値がT0で、区間が0〜600の範囲で数値的に解いています。tに時間、Teに解法結果として温度が得られます。ode45は微分方程式を数値的に解くコマンドです。ode45の具体的な使い方は、基礎編の第3回で説明します。5行目で、数値解で用いた時間tで解析解の(8)式の値を計算しています。6行目で両者をグラフにプロットしています。
このように、FreeMatを使うと、微分方程式を容易に解くことが可能です。極端な話、数値解法コマンドode45の使い方を知っていれば十分ともいえますが、次回は、ode45の基本となる数値解法のオイラー法とルングクッタ法について説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
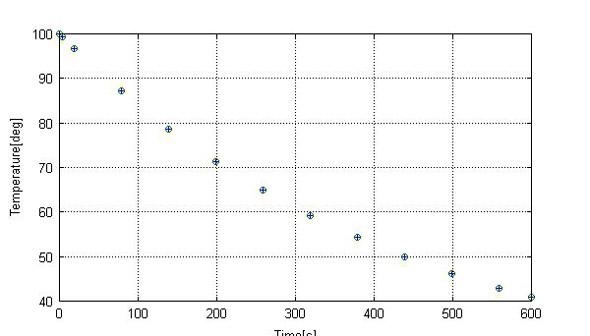 図3 解析解と数値解との比較
図3 解析解と数値解との比較






