ODE45で常微分方程式の初期値問題を解く:無償ソフトで技術計算しよう【シミュレーション基礎編】(3)(1/2 ページ)
4次のルンゲ・クッタ法をベースにした解法「ode45」は微分方程式を数値的に解くコマンド。今回はode45を使って微分方程式を数値的に解いていく。MATLABでの計算と比較もしてみた。
今回は、微分方程式を数値的に解くコマンド「ode45」の使い方を説明します。
筆者注:FreeMatはコマンド入力後にエンターキーを押すとコマンドを実行します。本連載ではエンターキーの記述を省略しますが、操作の際にはコマンド入力後にエンターキーが必要です。
odeとは
MATLABには「ode」と呼ばれる微分方程式解法のコマンドがあります。odeとは、「Ordinary Differential Equation」(常微分方程式)の略です。odeは常微分方程式を数値的に解くコマンドで、対応できる微分方程式に合わせていくつかの種類があります。ode45は4次のルンゲ・クッタ法をベースにした解法で、ほとんどの問題に対応できます。MATLABでは、初めにode45で試して、うまく行かない場合に別なodeで試すといった使い方をします。FreeMatにはode45のみ搭載されています。
ode45の使い方
ヘルプファイルを見てみましょう。ode45は「Numerical Methods」グループにあります。
function [t,y] = ode45(f,tspan,y0)
ode45 is a solver for ordinary differential equations and initial value problems. To solve the ODE y'(t) = f(t,y) y(0) = y0
over the interval tspan=[t0 t1], you can use ode45. For example, to solve the ode
y' = y y(0) = 1
whose exact solution is y(t)=exp(t), over the interval t0=0, t1=3, do
--> [t,y]=ode45(@(t,y) y,[0 3],1)
意味は、「ode45は常微分方程式の初期値問題を解くためのソルバーです。初期値がy(0)=y0で与えられるy'(t)=f(t,y)をt0からt1の範囲で数値的に解くといった場合にode45が使えます。例えば、dy/dt=yでy(0)=1をt0=0,t1=3の範囲で解くには(この問題の解析解はy(t)=exp(t)となりますが)、[t,y]=ode45(@(t,y) y,[0 3],1)と入力します」ということです。
ode45は、ode45(関数、解析範囲、初期値)と入力すると、解析結果を配列として返します。ここで、関数の与え方には、以下の3種類の方法があります。前回の説明で用いたdy/dx=cos(x)をx=0〜πの範囲で初期値y(0)=0で解くことを例に説明します。この場合、解析解はy=sin(x)になります。
inlineコマンドを用いる方法
下記のように、inlineコマンドを使い、任意の関数名でcos(x)を定義します。ode45には定義した関数名(この場合、f)を関数名に相当する引数の位置に記載すれば、定義された関数が渡されます。
--> f=inline('cos(x)');
--> [x,y]=ode45(f,[0,pi],0);
--> yy=sin(x);
--> plot(x,yy,'o-',x,y,'*-');grid('on');
1行目と2行目で、
という式を解いています。3行目と4行目でdy/dx=cos(x)の解析解y=sin(x)も、一緒にプロットした結果が図1になります。○が解析解、*が数値解になります。両者は良く一致していることが分かります。
図1を見ると、点の間隔が一定ではないことが分かります。
これは、ode45の解法による結果が必要な精度を満足するように、自動的に分割幅を設定しているためです。
図2は、数値で見た出力結果です。
xが列方向の配列であるのに対して、yは行方向の配列になります。後に説明するように、連立微分方程式の数値解では、yの1列目、2列目と列方向に計算結果が並びます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
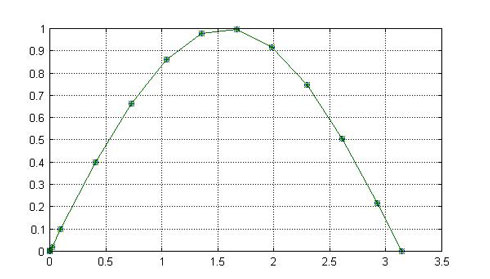 図1:dy/dx=cos(x)のode45による解法結果
図1:dy/dx=cos(x)のode45による解法結果 図2:ode45の出力結果
図2:ode45の出力結果





