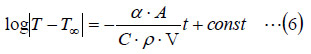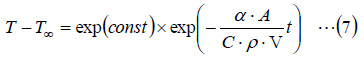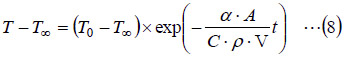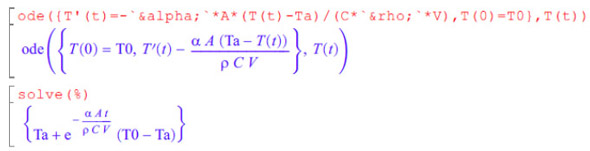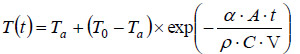AKB48……ではなくてODE45！ FreeMatだと微分方程式が容易に解ける：無償ソフトで技術計算しよう【シミュレーション基礎編】（1）（2/3 ページ）

[伊藤孝宏，MONOist]

微分方程式を解く

　（4）式は、物体内部に温度分布が存在しないという条件であれば成り立つため、放熱問題の基本式となります。しかしながら、このままでは実際の問題には使えないので、物体の温度Tを時間tの関数として求めます。これを「微分方程式を解く」といいます。では、（4）式を解いてみます。

　（4）式を下記のように変形します。

　（5）式の両辺を積分すると、

　ここで、constは積分定数です。T＞T∞であるから、

　ここで、t=0での温度（初期温度）をT0とすると、(7)式でt=0から、

となるので、

が得られます。

　（8）式は、物体の温度Tが物体の体積や密度、比熱などの諸元と時間ｔの関数で表されているため、必要な値を入れると、任意の時間での物体の温度を計算できます。

　微分方程式を解くことは、一般に手作業になりますが、シンボリック演算機能を持つ「Mathematica」、「Maple」、「MATLAB」（オプションが必要）、「MAXIMA」などのソフトでは、コンピュータが解いてくれます。

　例えば、（4）式をMATLABのシンボリック・マス・ツール（「Mupad」）で解いた例を下記に示します。

　1行目で、微分方程式と初期条件を定義しています。2行目は、Mupadが認識した内容を表示しています。次に、「solve（%）」とすると、微分方程式を解いてくれます。「solve」は「方程式を解け」というコマンドで、「％」は前式という意味です。

　4行目が解いた結果で、

という形で得られていて、これは（8）式と同じです。

　残念ながら、FreeMatにはシンボリック演算機能はありませんが、数値的に解く能力があります。微分方程式を数値的に解くとは、係数や初期条件を数値で与えて、微分方程式を満足するような結果を数値の配列として得ることをいいます。微分方程式を数値的に解く方法については、次回から説明します。