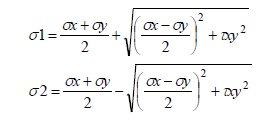固有値問題を用いて応力計算してみよう:無償ソフトで技術計算しよう【入門編】(4)(2/2 ページ)
固有値問題の解法
FreeMatは固有値問題が解けます。ここでは、材料力学で用いられる主応力を例に説明します。
「NASTRAN」「Abaqus」「ANSYS」といった有限要素法の解析ソフトで応力解析した場合、ミーゼス応力あるいは相当応力といった指標で評価することが多くあります。応力は力と力を受ける面との関係であり、応力の状態は行列となり、分かりやすい形では表示できません。そこで、大きさだけの値であるミーゼス応力が、材料の限度に対してどの程度の余裕があるかを比較する量としてよく使われます。
ミーゼス応力は下記の式で求められます。
ここで、σ1、σ2、σ3は主応力で、ミーゼス応力を求めるには主応力を求める必要があります。
主応力とは、図1に示すように応力とせん断応力が混在する場合、力を受ける面を適当に選べば、例えば図1で、nで示す法線に鉛直な面では、せん断応力を0とすることができます。このときのn方向の応力が主応力です。主応力とは、せん断応力が0となるような応力状態です。
主応力を求めるには、モール円(あまりよい思い出ではない方もいるかと思いますが……)により求める方法が(材料力学の教科書では)一般的です。ここで、固有値問題を用いて主応力を求めてみます。固有値問題とは、下記のような式を満たすベクトルxと固有値λを求めることです。Aは行列です。
FreeMatでは[v,r]=eig(A)と入力すると、vに配列Aの固有ベクトルの組み合わせが、rに固有値の組み合わせが返ってきます(V、rは任意の変数です)。では、試してみましょう。A=[1,2;3,4];[v,r]=eig(A);と入力します。
これで、vに固有ベクトル、rに固有値が入っています。
配列Aと固有ベクトル配列v、固有値配列rとは、A*v=r*vの関係にあり、バックスラッシュ演算により、r=v\A*vで、対角行列以外は0の行列が求まります。
例題:主応力を求めよう
では、例題として、下図の主応力を求めてみましょう。
eig([65,-33;-33,-48])と入力すると、-56.9313,73.9313と出力され、σ1=74MPa、σ2=-57MPaとなります。
結果が合っているか、主応力の公式で確かめてみましょう。下記の主応力の公式で計算すると、
σ1=73.9313、σ2=-56.9313と一致します。
例題は2次元の問題でしたが、3次元の応力においても同様に解くことが可能です。このように、FreeMatにより、材料力学の計算を軽減できることが分かるかと思います。もっとも、材料力学は、材料の応力状態を理解するためのもので、答えが得られれば十分というものではないことは言うまでもありません。
◇
入門編は今回で終了です。お疲れさまでした。次の連載は「グラフィックス編」ということで、グラフ作成に関する説明をしていきます。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
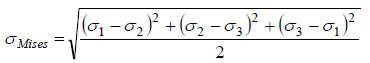
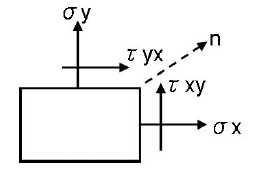 図1 応力状態
図1 応力状態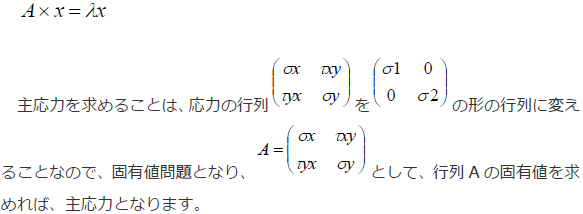


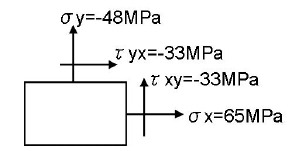 図2 応力状態
図2 応力状態