品質管理に必須の統計的手法「X-R管理図」「P管理図」の作り方：実践！ IE：現場視点の品質管理（14）（2/5 ページ）

[福田 祐二／MIC綜合事務所所長，＠IT MONOist]

（2）サンプルの平均値を算出する

　各サンプルの平均値（Xi）を計算します。計算の際、測定値の単位の1桁下までを求めます。

X₁＝ 381÷5＝76.2

X₂＝ 376÷5＝75.2

X₃＝ 372÷5＝74.4

（3）最大値と最小値の差を求める

　各サンプルの範囲（Ri）、すなわち、サンプルの最大の測定値と、最小の測定値との差を計算します。

R＝（xの最大値）−（xの最小値）

R₁＝79−73＝6

R₂＝78−71＝7

R₃＝76−73＝3

：

（4）平均値の算出

　Xの平均値（総平均）と、Rの平均値を計算します。計算の際、測定値の単位の2桁下までを求めます。

Xの総平均＝ΣX÷k＝（76.2＋75.2＋……＋76.0）÷20＝75.22

Rの平均値＝ΣR÷k＝（6＋7＋……＋4）÷20＝5.05

（5）CL、UCL、LCLを求める

　管理図に書き入れる管理線として、中心線（CL：Center Line）、上方管理限界線（UCL：Upper Control Limit）および下方管理限線（LCL：Lower Control Limit）を次の公式により計算します。

　計算式の中のA₂、D₃およびD₄は、サンプルの大きさnによって決まる定数で、「表2　X-R管理図用係数表」の値を使用してください。また、nが6以下の場合は、R管理図のLCLは考えませんので計算しません。

X管理図

　CL ＝Xの総平均 ＝ 75.22 ･････ 表1より

　UCL＝Xの総平均 ＋ A₂×Rの平均値 ＝ 75.22 ＋ 0.577×5.05 ＝ 78.14

　LCL＝Xの総平均 − A₂×Rの平均値 ＝ 75.22 − 0.577×5.05 ＝ 72.30

R管理図

　CL ＝Rの平均値 ＝ 5.05 ･････ 表1より

　UCL＝D₄×Rの平均値 ＝ 2.115×5.05 ＝ 10.68

　LCL＝D₃×Rの平均値 ＝　―　･････ nが6以下のため計算しない

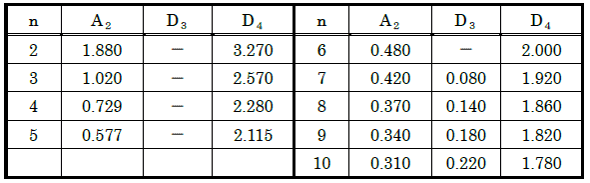表2　X-R管理図用係数表