ワーストケースと二乗和平方根って、何?:公差解析 基本中の基本(2)(3/4 ページ)
ユー! もーイッカイやってみよう! いまの溝の寸法範囲で、±(プラスマイナス)公差に置き換えてミテ!
デイちゃんの疑問は無視して、おじさんはマイペースに説明を進めます……。
10.15±0.15mmよ
入れる部品も、やってミテYO!
4.85±0.05mmになるよ!
ユーたち計算速いネ〜。じゃあ10.15mmから4.85mmを2つ分引いてミテYO!
10.15−(4.85×2)だから、0.45mmだよ。ねぇねぇ、おじさん何してるの? いま?
あとは溝の公差と2つの部品の公差をそれぞれ二乗して足して! そこのボーイ!
オレのこと? ふふっ、仕方ねーな。歴史だけじゃなく、計算も得意なんだ。(0.15^2+0.05^2+0.05^2)で0.0275だぞ
それを平方根で返すと0.165831……ダネ! 丸めて0.17にするよ! スキマは0.45±0.17mmにナル可能性もあるんだYO!
0.28〜0.62mmの範囲!? だったらまだ余裕がありそうじゃないですか! おじさん、何でそうなるんですか?
ミーは、天・使・さ・ん! いま、ミーは『ワーストケース』と『二乗和平方根』の2種類の方法で計算したんだYO!
『ワーストケース』? 『じじょーわヘイホーこん(二乗和平方根)』? 何それ!?
ワーストケースっていう言葉から、何を想像スル?
これは日本人が苦手だといわれる英語。日本語に直訳すると『最悪の状態』!?
イエス! 公差の最悪値を積み上げて、サイアクの状態を想定スルんだYO!
でもさ、その“サイアク”な部品同士がたまたま出会って組み立てるっていう可能性はどれだけあるのかなぁ〜。超レアだよね!!
同じ製品をタップリ作るとき、そこで出会う確率は超レアかもしれないネ! でも、ちょっとの数しかその製品を作らないから、どんな寸法で製品ができるのか傾向がつかみにくいとか、人の命にかかわるものを作っているとか……場合によってはサイアクな状況を考えておかないといけないこともあるんだYO!
そっかぁ。じゃあさ、『二乗和平方根』は何が違うの?
カンタンにいうと、その超レアな確率には、チョット目をつぶって、起こり得る可能性の範囲内で積み上げたってカンジかな?
……よく分かんないわよ
ユー! ……ゆうねぇ〜……なんちゃって! エヘッ!
……
例えばネ、さっきの部品をイッパイ加工するでしょ? そのときに公差の中心を狙って加工したデータを集計すると、こーんなふうにならない? デイちゃん!(図2)
うーん。まぁそんな感じかなぁ……
ここで線を引いちゃおう(図3)。そうすると、この山のミミみたいなところ(図3 黄色い箇所)、この割合って全体の0.3%なの。1000個作った中の3個の不良が、出ルか出ナイかの領域! この少ない確率は気にしないのが、二乗和平方根ダヨ! だからさっきの0.45±0.17っていうスキマも、0.3%は不良になるのが前提の数字だYO! だからワーストケースよりも結果が良いのさ!
分かったような、分かんないような感じね。何でこんな計算が成立するの?
説明シヨウ! 分散の加法せ……
キュルルルルルル〜。
工作室に響く、とぼけた音。この正体は?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
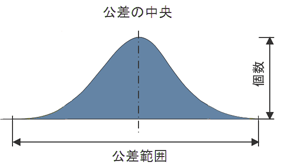 図2 加工部品の寸法分布
図2 加工部品の寸法分布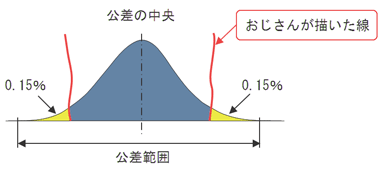 図3 1000個作った中の3個の不良が、出ルか出ナイかの領域!
図3 1000個作った中の3個の不良が、出ルか出ナイかの領域!





