チリも積もれば予想外:「失敗学」から生まれた成功シナリオ(2)(2/2 ページ)
だから、ご利用は計画的に
「そんなに大きく膨れ上がるのか」と嘆息するのは複利計算(*5)である。例えば「1530万円借りたとき、年利3%で30年ローンを組みましたが、1月にいくらずつ払えばいいでしょうか」という問題。
月ごとの利息0.25%で360カ月の複利計算になって、計算自体はややこしいので略すが、月当たり6万4505円になる。これは15年前に筆者がマンションを購入するとき、親から借りた借金の例である。贈与にならないように、税理士に相談して当時のローンよりも1%低めの利息を設定したが、その後の銀行の預金金利がほぼ0%になったことを考えると、疲労試験のように小さな力で家計を打撃し続けた。
このとき、図3に示すように、仮に利息が0%だと1530万円を360で割ればよいから4万2500円になる。それと上述の値と比べてみると、3%にしただけで1.52倍の総計2322万円も払わなければならないことが分かる。利息をたった3%増やしたら、返済総額は50%増しになった。
これが6%だと、3302万円で2.16倍、その倍の12%だと5666万円で3.70倍も払うことになり、普通は元利よりも利息総額の方が多いではないかと気が付く前に自己破産に至る。消費者金融で借りると、利息制限法の上限は15%だから6965万円となって4.55倍、以前の出資法の上限の29.2%だと、計算するのも恐ろしいが、1億3405万円で8.76倍となる。こんなのを借りていたら、身の破滅である。
複利計算は年月を長くしても膨大な金額になる(図4)。例えば、アメリカの富豪は20世紀の100年間に財産を1000倍に増やしているが、さて年何%の利回りで投資したか、という問題。このとき、2つの有名な近似式を使うと簡単に解ける。まずは、物理学ではよく使う手だが、(2の10乗)の1024が(10の3乗)の1000とほぼ等しいという近似式である。これを使うと、100年で1000倍にするには10年ごとに2倍にすればよいことが分かる。
もう1つ経済学でよく使う手であるが、複利で2倍になる年数と、年利(%)の積は72になるという近似式を使う。実際にその積を計算してみると、年利1%だと69.7、5%だと71.0、8%だと72.0、14%だと74.0となり、不思議なことに積は大体それくらいの数値で一定である。だから10年で2倍になるには、72割る10の年利7.2%で運用すればよいことが分かる。米国で運用すれば、7.2%はそれほど難しい値ではない。結局、戦争や天災がない限り、金持ちは金持ちのままである。欧州ではスイスの金融機関を使えば、戦争に負けた国の金持ちさえ、勝った国に投資してもうけることも可能である。
古き時代のボーナス交渉術
複利計算と同じように、等比級数も結果が急増し、直観を超える。
その昔、曾呂利新左衛門(そろり しんざえもん)は、太閤様が何でも褒美を取らすというので、最初の1日に1文の銭を貰い、次の日から2文、4文と2倍ずつ増やして1カ月間もらい続けたいと頼んだそうである。太閤さんは「欲のない奴だ」と笑って許したが、そのうちに金蔵が空になって青くなった、という話である。
2の等比級数だから級数の和を計算すると、30日後には(2の30乗)−1文だけの銭がもらえる。上述した(2の10乗)の1024が(10の3乗)の1000とほぼ等しいという近似式を使うと、(2の30乗)は(10の9乗)に等しく、1億と同じになる。つまり1億文もらうのであるが、6000文が1両だから、総計1万6000両になる。1両は現在の10万円くらいだから、16億円である。臨時収入にしては多過ぎるが、頓智(とんち)の勝利である。
紙も積もれば月に届く!?
次の問題は、図5に示すように、紙を2つに切っては重ねる、という動作を何回繰り返したら、重ねた紙の束は月に届くか、という問題。紙の厚みを50μm=0.05mm、月へまでの距離は38万kmと仮定する。2の等比級数だから、X番目までの総計は(2のX乗)−1となり、つまり、(2のX乗)=38万km÷0.05mm=8×(10の12乗)の式を解けばよい。(10の12乗)は(10の3乗)の4乗だから、近似すると(2の10乗)の4乗で、(2の40乗)となる。8は(2の3乗)だから、上述した近似式を用いると8×(10の12乗)=(2の43乗)となる、つまり、2つに切って重ねる動作を43回も繰り返せば月に至るのである。チリも積もれば山となる、である。(次回に続く)
編集部注
*5 複利計算:借金した金額に利子を加えた額に対して、利子を計算すること。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
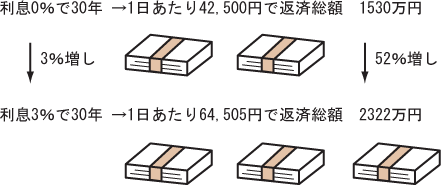 図3 利息を3%増やしたら、返済総額は50%は増えた
図3 利息を3%増やしたら、返済総額は50%は増えた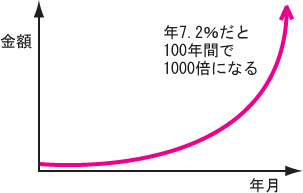 図4 複利計算は、年月を長くすると、膨大な金額になる
図4 複利計算は、年月を長くすると、膨大な金額になる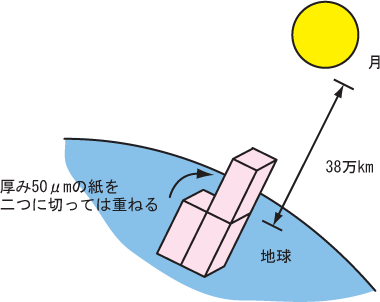 図5 紙を2つに切って重ねていくと、 何回で束が月に届くか
図5 紙を2つに切って重ねていくと、 何回で束が月に届くか






