冷却系の設計を自分でやってみる企画を総括する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(19)(3/4 ページ)
量子力学
連載の中で、何カ所か量子力学に関する記述を混ぜてしまいました。少しおふざけが過ぎたと反省しています。
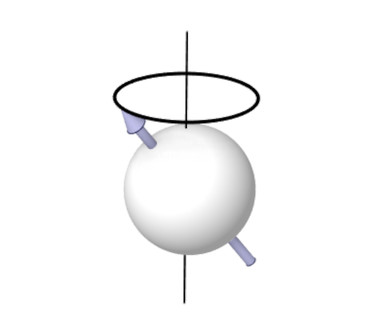
過去のシリーズ(連載「CAEと計測技術を使った振動・騒音対策」の第6回)では、医用画像診断装置であるMRIについて触れました。その際に「原子核はコマのように回転していて、歳差運動をしているといわれている。しかし、原子核が小さな磁石で、本当に球の形をしているかどうか、あるいは地球のように自転しているかは見て確認したわけではなく、この説明もコマを使ったアナロジーにすぎない」と述べ、コマの歳差運動による説明は“ただのアナロジーにすぎない”と断罪しました。
つまり、水素原子核が図3のような動きをするはずがないと説明したのでした。
しかし、その後に読んだある文献(参考文献[1])によって、少し考えが変わりました。スピンの方向を観測すると、「上向き」か「下向き」のどちらかしか得られません。つまり、歳差運動そのものは観測されないということです。
「上向き」と観測されたら「1」と、「下向き」と観測されたら「−1」と記録していきます。これを何度も繰り返し、その平均を取るとゼロになります。
ここで、水素原子を強いZ軸方向の磁場の中に置き、ある周波数の電波を照射すると(MRI装置ですね)、観測結果として「1」が出る割合が増える場合があります。
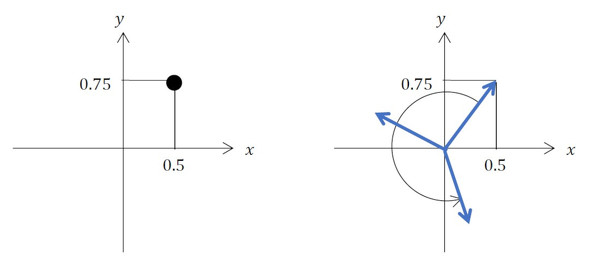
例えば、x方向スピンの観測結果の平均値がゼロではなく0.5くらいになったとしましょう。では、y方向スピンはどうかというと、x方向スピンが観測されたからといって、y方向の観測結果が全てゼロになるわけではありません。y方向でも1か−1が観測され、その結果にも偏りが生まれます。ここでは、その平均値を0.75と仮定します。
このとき、図4のxy平面上に座標(0.5,0.75)をプロットし、原点と結ぶ矢印(ベクトル)を描きます。
ポイントはここからです。スピン観測値の平均は時々刻々と変化するため、この矢印は原点を中心に回転します。この回転周波数こそが、いわゆるラーモア周波数です。
スピンの方向自体は「上向き」か「下向き」ですが、原子核は小さな磁石として振る舞っているかのように見えます。そのため、近くに受信コイルを置くと、このベクトルの回転に伴って起電力が発生し、あたかも原子核から電波が放出されているかのように観測されるのです。
このように考えると、筆者が30年近く説明できずにいたMRI装置の撮影法における、90度パルスや180度パルスの量子力学的説明ができそうです。
以前、「コマの歳差運動はただのアナロジーだ」と断じましたが、この考えを訂正したいと思います。おそらく半分はアナロジーで、もう半分くらいは量子力学で説明できる気がしています。……これ、間違っていますかね?
参考文献:
- [1]J.J.サクライ、ナポリターノ|現代の量子力学(上) 第3版|訳:桜井明夫、常次宏一(2024)
ベルヌーイの式
紙面が余りましたので、前回紹介した連続の式に続き、ベルヌーイの式(Bernoulli's equation)について説明します。いろいろな計算式がありますが、水を流す冷却系の設計では、ベルヌーイの式と連続の式を組み合わせて使うことが多かったようです。
ちなみに、熱伝導のフーリエの法則を見いだしたフーリエ氏と、フーリエ級数を考え出したフーリエ氏は同一人物ですが、ベルヌーイ氏は3人いるので注意が必要です。ここで紹介するベルヌーイの式は、ダニエル・ベルヌーイ氏によるものだそうです。
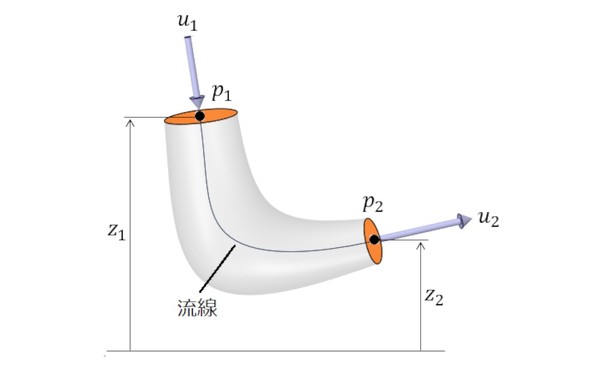
図5に示すように、流路内の1本の流線の上流と下流における流速、圧力、高さを記号で表すと、ベルヌーイの式は式1となります。
この式の最後の項はエネルギー損失を表します。式1をρg倍すると、式2になります。
この式では、最後の項が圧力損失として表されます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

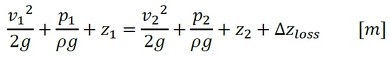 式1
式1





